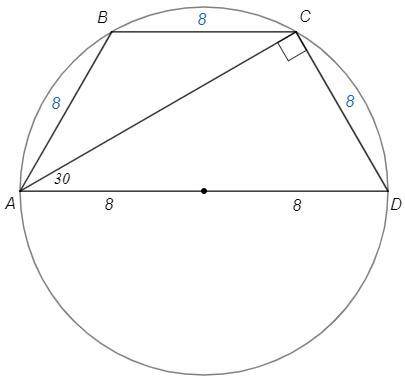
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)
ответ: ∠АDС=∠АВС=68*2=136*;
∠BCD=∠BAD=2*22=44*.
Объяснение:
Условие на русском:
"найти углы ромба, если угол образован меньшей диагональю ромба с одной из сторон равен 68° ".
Из свойства ромба знаем, что диагонали пересекаются под углом 90*.
Диагонали образуют в ромбе четыре равных треугольника..
Рассмотрим треугольник АОВ. Угол АВО=68*. Сумма углов в треугольнике равна 180*. Тогда угол ВАО=180*-(68*+90*)=22*.
Значит углы ромба равны:
∠АDС=∠АВС=68*2=136*;
∠BCD=∠BAD=2*22=44*;
Объяснение на украинском:
З властивості ромба знаємо, що діагоналі перетинаються під кутом 90*. Діагоналі утворюють в ромбі чотири рівних трикутника.. Розглянемо трикутник АОВ. Кут АВО=68*. Сума кутів в трикутнику дорівнює 180*. Тоді кут ВАО=180*-(68*+90*)=22*. Значить кути ромба рівні: ∠АDС=∠АВС=68*2=136*; ∠BCD=∠BAD=2*22=44*;
2) Если прямая имеет с окружностью общую точку, а радиус, проведенный к точке пересечения окружности, перпендикулярен этой прямой, то прямая является касательной к окружности.