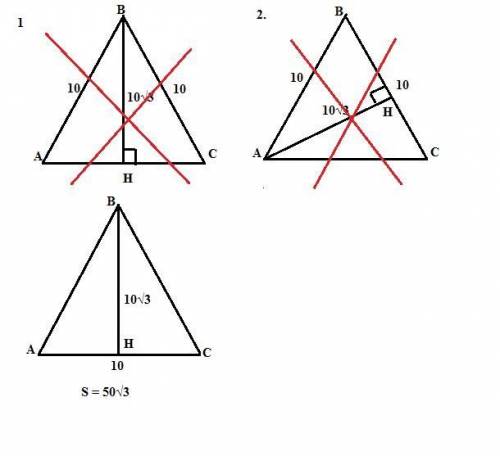
S = 50√3 см².
Объяснение:
Предположим, что высота равнобедренного треугольника равная 10√3, проведена к основанию. Это противоречит условию, так как гипотенуза не может быть меньше катета.
Предположим, что боковые стороны равнобедренного треугольника равны 10 см, а высота проведена к боковой стороне. Это так же противоречит условию, так как гипотенуза не может быть меньше катета.
Остается вариант, при котором сторона основания треугольника равна 10 см. Тогда высота является и медианой (по свойству высоты равнобедренного треугольника, проведенной к основанию) и тогда
S = (1/2)·10·10√3 = 50√3 см².
+2 задание:
Рассмотрим треугольник DME:
предположим ,что угол DME - тупой (будет смежным с острым углом этого треугольника) и угол DEM - острый (так как двух углов тупых не может быть в треугольнике по определению и признаку треугольника) .
Если напротив большего угла в данном треугольнике лежит самая большая сторона,то DE>DM.
Что и требовалось доказать.
+3 задание:
уголN=180-(69+37)=74
уголMNP=74/2=37
угол NPM=180-(37+69)=74
уголNPK=180-(37+37)=69
угол MPN=74
уголNPK=69
уголMPN больше угла NPK, то MPменшеРК
+4 задание:
С=180-76-66=38
ЕК - биссектриса => КЕС=38
С=КЕС => треугольник КЕС равнобедренный, КС=ЕК
В треугольнике против большего угла лежит большая сторона
DEK<D => DK<EK=КС DK<КС
Тогда х+х+100=180,
2х=180-100,
2х=80,
х=80°:2=40°.
ответ: 40°, 40°, 100°.