
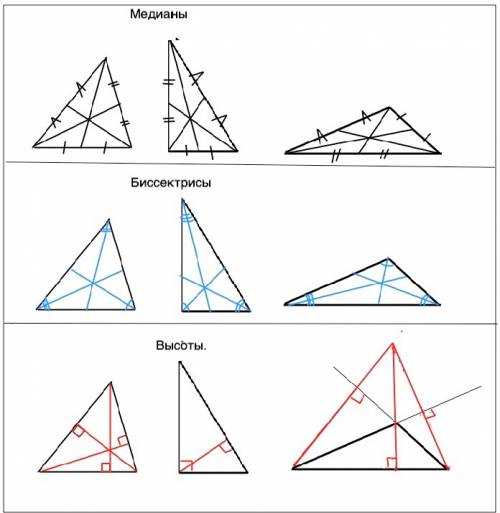
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
38
Объяснение:
1) Так как по условию сказано, чо угол ACB=90 градусов, то получается, что треугольник ABC - прямоугольный.2) По условию сказано, что СD-медиана, то есть по особому свойству медианы в прямоугольном треугольнике получаем, что AD=DB=DC (Особое свойство медианы: медиана соединяет одну сторону с серединой другой стороны).3) Треугольники ADC и BDC равнобедренные, так как AD=DB=DC. А в равнобедренном треугольнике: если стороны равны, то и углы равны, то есть в треугольнике BDC: угол B = углу DCB = 52 градуса.4) Угол ACD = угол C - угол DCB;Угол ACD = 90 - 52 =38 градусов.ответ: Угол ACD = 38 градусов.