Объяснение:
"2. Один из углов, образованных при пересечении двух прямых, равен 63°. Найдите градусные меры остальных углов.
3. Один из смежных углов на 52° больше второго. Найдите эти углы.
4. На рисунке 265 AB =CD, А В C D E AC = CE. Докажите, что Рис. 265 BC = DE.
5. Углы АВС и свD смежные, луч Вм — биссектриса угла ABC Kyr ABM в 2 раза больший угол свD. Найдите углы ABC i CBD. Точки A, Bi слежат на одной прямой, AB = 15 см, отрезок Ас в 4 раза больше отрезка вс. Найдите отрезок АС. ответ: Объяснение: "2. Один из углов, образованных при пересечении двух прямых, равен 63°. Найдите градусные меры остальных углов. 3. Один из смежных угл"
2) При пересечении двух прямых образуются четыре угла: два смежных и два накрест лежащих.
Сумма смежных равна 180*, а накрест лежащие равны между собой.
Поэтому смежные углы: 180*-63*=117*, а вертикальные равны данным углам: один равен 63*, а другой - 117*
3) Пусть один из смежных углов равен х*. Тогда второй равен х+52*. Их сумма равна 180*.
х+х+52*=180*.
2х=128*.
х=64*. - меньший угол
Больший угол равен 64*+52=116*.
ответ: 64* и 116*.
4) Извините, но рисунка не наблюдаю... ???
5)
Объяснение:
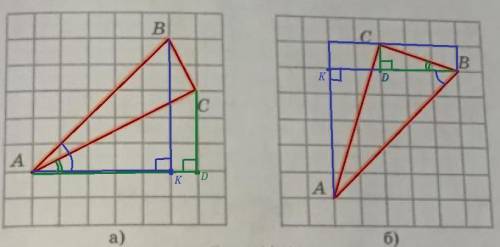
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
а)
tg∠A = BC / AC = 3/6 = 1/2
ctg∠A = AC / BC = 6/3 = 2
б)
tg∠B = AC / BC = 4/6 = 2/3
ctg∠B = BC / AC = 6/4 = 3/2
№2
Тангенс угла в прямоугольном треугольнике -это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
tg(a-β)=tga-tgβ/1+tga×tgβ; tg(a+β)= tga+tgβ/1-tga×tgβ
a)tg ∠BAC = tg(∠BAD-∠CAD) =tg∠BAD- tg-∠CAD/1+tg∠BAD×tg∠CAD=∠BAD= BK/AK=5/5=1; tg∠CAD= CD/AD=3/6=1/2=1-1/2/1+1×1/2=1/2/3/2=1/3
ctg∠BAD=1/tg∠BAD=1/1/3
b) tg∠ABC=tg(∠CBD+∠KBA) =tg∠CBD+tg∠KBA/1-tg∠CBD×tg∠KBA=tg∠CBD=CD/BD=1/3; tg∠KBA=AK/BK=5/5=1=1/3+1/1-1×1/3=4/3/2/3=4/2=2
3х+4х+5х=48
12х=48
х= 4
12, 16, 20 - стороны треуг.