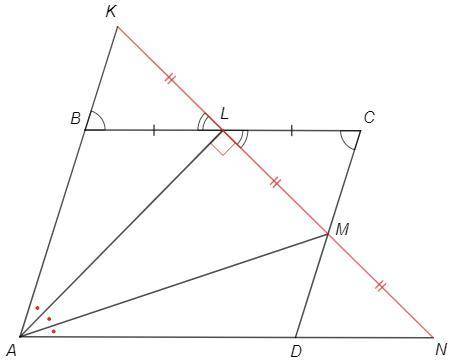
L, M - середины сторон.
Продлим LM до пересечения с AB в точке K
BL=LC (по условию)
∠KBL=∠C (накрест лежащие при AB||CD)
∠KLB=∠MLC (вертикальные)
△KBL=△MCL (по стороне и прилежащим углам) => KL=LM
△KAM: AL - биссектриса (по условию) и медиана, следовательно и высота, ∠ALM=90.
Продлим LM до пересечения с AD в точке N
Рассуждая аналогично, △MDN=△MCL => MN=LM =>
△NAL: AM - биссектриса/медиана, следовательно и высота, ∠AMN=90
Из точки A можно провести только один перпендикуляр к прямой LM. Следовательно данная конфигурация невозможна.
∠BAD = 68
∠BCD = 92
∠B = 100
∠D = 100
Объяснение:
∠B = ∠D , т.к. напротив лежащие
∠BAD = 68 , т.к. ∠A = 34, а т.к. прямая АС делит угол параллелограмма на два, то, угол ∠А = 34 * 2 = 68, т.е. угол ∠А изначально был 68
∠BCD = 92, т.к. т.к. ∠С = 46, а т.к. прямая АС делит угол параллелограмма на два, то, угол ∠С = 46 * 2 = 92, т.е. угол ∠С изначально был 92
И проверим, правильно ли всё:
Складываем получившиеся углы ∠B + ∠D + ∠A + ∠C = 100°+100°+68°+92° = 200°+160°= 360°
Всё верно, т.к. параллелограмм имеет сумму углов 360°
Формула нахождения высоты проведенной к гипотенузе прямоугольного треугольника:
H=ab/с где H – искомая высота, a и b катеты треугольника, с – гипотенуза.
Н=15*20/25=12 см