должно быть в ответе опечатка, ответ получается 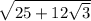
Объяснение:
1) Поскольку сторона СВ=АВ, то достроим ΔABM так чтобы он был равен ΔCNB. ΔMNB получился равнобедренный.
2) ∠ABC = 60 по условию, но тогда ∠NBM тоже = 60, тогда на два оставшихся угла приходится 180-60=120, а поскольку Δ равнобедренный, то 120:2=60, т/е Δ получается равносторонний. т.е ∠NMB=60
3) теперь рассмотрим ΔANM - мы знаем все его стороны, значит по теореме косинусов сможем найти и углы
AN²=AM²+NM²-2AM×NM×cosAMN
25=16+9-2×4×3×cosAMN
0=24×cosAMN ⇒ cosAMN=0⇒∠AMN=90°
4) ∠AMN=90° + ∠NMB=60 ⇒ ∠ AMB = 150°
5) по той же теореме косинусов сможем найти сторону AB в ΔАВМ, тогда и задача будет решена
АВ²=16+9-2×4×3×cos150°
как же найти cos150°? в таблице значения только до 90°. Здесь нам формулы приведения. cos150° = сos (π/2+60)=sin 60°=√3/2
АВ²=16+9-2×4×3×√3/2
АВ=√(25-24×√3/2)
АВ=√(25-12√3)
Р(АВК)=16 , Р(ВКС)= Р(АВК) , так как ΔАВК=ΔВКС по двум сторонам и углу между ними (АВ=ВС , ВК - общая , ∠АВК=∠СВК)
Р(АВС)=Р(АВК)+Р(ВСК)-2*ВК=2*Р(АВК)-2*5=2*16-10=22
2) ΔDEF: ДК - биссектриса ⇒ ∠КDЕ=∠КDF=68°:2=34°
∠F=180°-(∠EDF+∠DEF)=180°-(68°+44°)=68°
ΔDKF: ∠DKF=180°-(∠KDF+∠DFK)=180°-(34°+68°)=78°
3) Точки, лежащие на серединном перпендикуляре к отрезку, равноудалены от концов этого отрезка ⇒ DC=DB=4 см.
АВ=AD+DB=AD+4 ⇒ AD=AB-4=7-4=3 (см) .