1) см. рис
А и А1 точки пересечения окружностей с центрами О и К
АР перпендикуляр на продолжение ОК
АР=у
ОР=х
ОА=4
КА=8
ОК=6
х²+у²=4²=16
(х+6)²+у²=8²=64 ⇒ у²=64-(х+6)², подставляем в первое
х²+64-(х+6)²=16
х²+64-х²-12х-36-16=0
12х=12
х=1
у=√(16-1)=√15
l -расстояние от т.О до ц. окр. М касающихся одновременно двух данных, т.е. в т.А и А1 (необходимо найти МА)
МА²=(х+l)²+у²=(1+l)²+15
2)
АВС - треугольник, а=60, В=50, С=70, т.Н пересечение
АА1, ВВ1, СС1 высоты.
<АНС1=<СНА1=<3 (вертикальные)
<BHC1=<CHB1=<1 (вертикальные)
<BHA1=<AHC1=<2 (вертикальные)
ΔВНА1 подобен ΔВСВ1 ⇒<BHA1=<С=70
ΔВНС1 подобен ΔВАВ1 ⇒<BHC1=<А=60
ΔСНА1 полобен ΔСВС1 ⇒<СНА1=<В=50
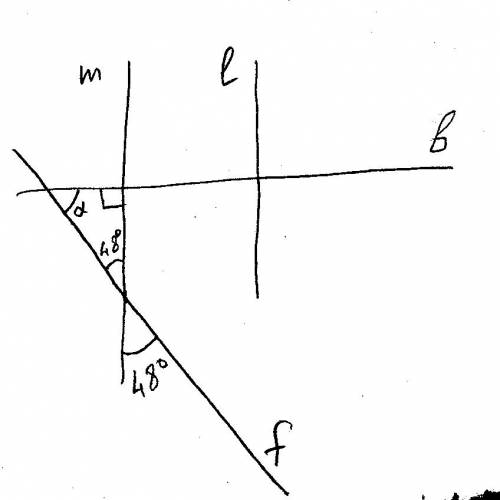
3) см рис. 2
<α=180-90-48=42°
Если АВ=ВС, значит этот треуг-к равнобедренный, а в равнобедренном треуг-ке высота, проведенная к основанию,является и биссектрисой, и медианой. Sтреуг-ка=1/2 *а*h, где а-основание, h-высота, отсюда получаем:
а=Sразделить на 1/2 h, а=60/(1/2 *12), а=10,то есть основание АС=10, а АН=5, поскольку ВН -это и медиана. В общем получили,что в треуг-ке АВН угол ВНА = 90 градусов, сторона АН=10, ВН=12. АВ-гипотенуза, а квадрат гипотенузы=сумме квадратов катетов, значит АВ^2=5^2 + 12^2=25+144=169, значит АВ= корень квадратный из 169, это будет 13.
ответ: АВ=13.
сумма остальных 2-х =180°, пусть меньший=х, больший=2х,
х+2х=3х=180°,х=180/3=60°-меньший, 2х=2*60=120°-больший угол