S=24 cм2
Объяснение:
S=1/2(3+7)*h h=h1+h2
О - точка пересечения диагоналей. Диагонали делятся точкой пересечения на отрезки пропорционально отношению оснований трапеции.
Имеем треугольник АОД со сторонам 7 см и 6/(7+3)*7=4,2 см и 8/10*7=5,6 см По трем сторонам определяем площадь этого треугольника
p = a + b + c 2 = 1 /2 (7 + 4.2 + 5.6) = 8.4
S = √p(p - a)(p - b)(p - c) =
= √(8.4)(8.4 - 7)(8.4 - 4.2)(8.4 - 5.6) =
= √(8.4)·(1.4)·(4.2)·(2.8) = √138.2976 = 11.76 (см)2
h1=11.76/7*2=2*1.68=3,36 см
Второй треугольник ВОС со сторонам 3 см и 6/(7+3)*3=1,8 см и 8/10*3=2,4 см По трем сторонам определяем площадь этого треугольника
p = a + b + c 2 = 1 2 (3 + 1.8 + 2.4) = 3.6
S = √p(p - a)(p - b)(p - c) =
= √(3.6)(3.6 - 3)(3.6 - 1.8)(3.6 - 2.4) =
= √(3.6)·(0.6)·(1.8)·(1.2) = √4.6656 = 2.16 (см)2
h2=2.16/3*2=0.72*2=1,44 см
h=3,36+1,44=4,8 см
S=4.8*(3+7)/2=24 cм2
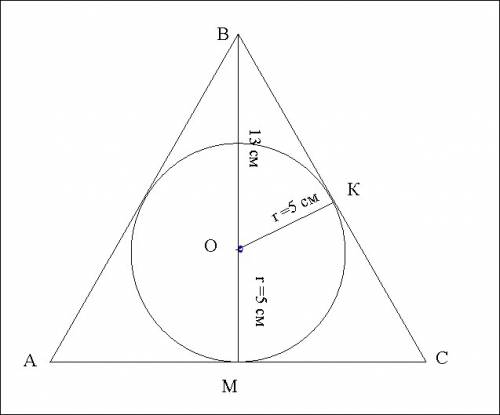
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см