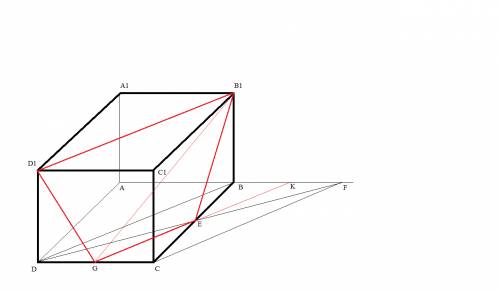
сделаем построение по условию
точка G - середина отрезка CD
точки B1, D1,G образуют плоскость GB1D1
дополнительные построения
прямая (BD) параллельна (B1D1)
прямая (CF) параллельна (BD)
прямая (GK) параллельна (BD)
прямая (CB) -секущая для параллельных прямых (BD) ,(GK), (CF)
по теореме Фалеса, прямая (CB) отсекает пропорциональные отрезки DG=GC и CE=EB
по теореме Пифагора
GE^2 = GC^2+CE^2=(D1C1/2)^2+(B1C1/2)^2 =( (D1C1)^2+(B1C1)^2 )/4 = (B1D1)^2 / 4
GE = B1D1/2 - отрезки GE и B1D1 НЕ РАВНЫ
прямая (GK) параллельна (BD) , а значит и (B1D1) и проходит через точку G в плоскости GB1D1
следовательно прямая (GK) принадлежит плоскости GB1D1
точка E - пересечение (GK) и (CB)
точки Е и B1, а значит и отрезок EB1 принадлежат плоскости GB1D1
искомое сечение - четырехугольник GD1B1E ,
противоположные стороны B1D1 и EG параллельны и не равны.
Основной признак ТРАПЕЦИИ:
четырёхугольник является трапецией, если его параллельные стороны не равны.
ДОКАЗАНО
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см