Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
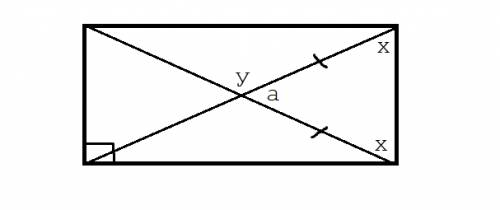
КР=MN и КР║MN
КМ=NР и КМ║NР
∠К=∠N
∠М=∠Р
Рассмотрим треугольники КВР и МNА.
KB=NA - это дано по условию задания.
КР=MN - это мы выяснили выше
∠K=∠N - это мы выяснили выше
А эти равности дают нам право утверждать, что треугольник КВР=треугольнику МNА.
А это означает, что BP=MA.
Также из равности треугольников можно утверждать, что
∠KBP=∠NAM
∠BPK=∠AMN.
Сумма мер двух смежных углов равна 180°, значит
∠MBP+∠KBP=180°, отсюда ∠MBP=180° - ∠KBP
∠PAM+∠NAM=180°, отсюда ∠PAM=180° - ∠NAM
Поскольку ∠KBP=∠NAM, а значит
∠MBP=∠PAM
Поскольку ∠BPK=∠AMN и ∠KMN=∠KPN, тогда
∠KMA=∠NPB, так как
∠KMN=∠KMA+∠AMN, отсюда ∠KMA=∠KMN-∠AMN
∠KPN=∠BPK+∠NPB, отсюда ∠NPB=∠KPN-∠BPK
KM=KB+МB, отсюда MB=KM-KB
NP=NA+AP, отсюда AP=NP-NA
Поскольку KM=NP, а KB=NA, значит
MB=AP.
Поскольку KM║NP, то и MB║AP.
Получаеться, мы выяснили, что
BP=MA
∠MBP=∠PAM
∠KMA=∠NPB
MB=AP
MB║AP.
Из всего этого мы можем сделать вывод, что АМВР - это параллелограмм, поскольку у него противоположные стороны и углы равны.