SABCD -правильная четырехугольная пирамида. Постройте сечение пирамиды плоскостью, проходящей через DO (точка О-внутренняя точка отрезка SC) и перпендикулярной плоскости ABC.
Если искомая площадь перпендикулярна плоскости АВС, то она перпендикулярна плоскости АВСD.
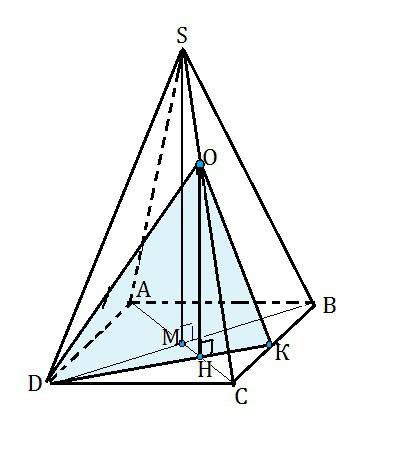
Проведем диагональное сечение АSС пирамиды .
О лежит на ребре SC и принадлежит этому диагональному сечению.
Опустим в плоскости ∆ ASC из О перпендикуляр ОН на АС (он лежит в плоскости диагонального сечения, перпендикулярной основанию, параллелен высоте пирамиды, и потому перпендикулярен её основанию).
Через D и Н проведем прямую до пересечения с ВС в точке К.
Соединим D, О и К.
Через 3 точки можно провести плоскость, притом только одну.
Плоскость ∆ DОК - сечение пирамиды.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Плоскость ∆ DОК проходит через ОН, перпендикулярный плоскости основания, и является искомым сечением
(AM + BM)² = (BH + HC)² + (AL + LC)².
По условию:
AM = AL = 10;
BM = BH = 3.
OLHC — квадрат, так как все углы прямые и смежные стороны равны: OL = OH = r.
Значит, OL = OH = HC = LC = r.
Получаем уравнение.
(10 + 3)² = (3 + r)² + (10 + r)²,
13² = 3² + 6r + r² + 10² + 20r + r²,
2r² + 26r - 60 = 0,
r² + 13r - 30 = 0,
По теореме Виета r = 2, r = -15.
-15 — построений корень.
Отсюда r = 2.
ответ 2.