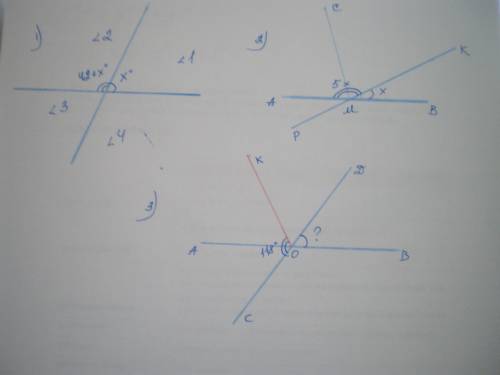
1.
Пусть ∠1=х°, тогда ∠2=(42+х)°, что в сумме составляет 180° по определению смежных углов. Составим уравнение:
х+42+х=180; 2х=138; х=69.
∠1=∠3=69°; ∠2=∠4=69+42=111°.
2. Дано: ∠ВМК и ∠АМК - смежные, МС - биссектриса ∠АМК. Найти ∠СМК и ∠СМВ.
Пусть ∠ВМК=х°, тогда ∠АМК=5х°, что в сумме составляет 180°.
х+5х=180; 6х=180; х=30.
∠ВМК=30°, ∠АМК=30*5=150°
∠СМК=1/2 ∠АМК = 150:2=75°
∠СМВ=∠СМК+∠ВМК=75+30=105°
3. Дано: АВ и СD - прямые, ∠СОК=118°, ОК - биссектриса ∠АОD. Найти ∠ВОD.
∠КОD и ∠СОК - смежные, значит, их сумма составляет 180°.
∠КОD = 180-118=62°
∠АОК=∠КОD=62° (по определению биссектрисы)
∠АОК+∠КОD=62+62=124°
∠ВОD=180-124=56°
Уточним, что окружность не может быть внутри угла АСО, так как О - ее центр, а центр вписанной окружности лежит на биссектрисе угла, в который она вписана. Биссектриса же проходит строго посередине угла.
Будем находить угол АСD и угол АСО- его половину.
Смотрим рисунок.
С - точка вне окружности.
Из нее к окружности идут две касательные СА и СD. Расстояния от С до точек касания с окружностью равны.
Соединим точки касания с центром О. Отрезки АО и DО - перпендикуляры.
Поэтому
∠ САО+∠СDO=180º.
Сумма углов четырехугольника равна 360º.
∠АСD+∠AOD=180º.
Центральный ∠АOD опирается на дугу АD и равен 140º.
∠АСD=180º-140º=40º.
Его половина ∠АСО=40:2=20º
Длина АД=12 дана для понимания процесса- что она больше АВ,
соответственно, смеем предположить, что Е лежит на ВС,F лежит на АД.
биссектрисы углов параллелограмма отсекают на сторонах, которые они пересекают, отрезки , равные меньшим сторонам, т.е.
ЕС=СД
FД=СД, тогда ввиду параллельности ВС и АД получим параллелограмм ( да и еще ромб) ЕСДF, т.е. ЕF=3