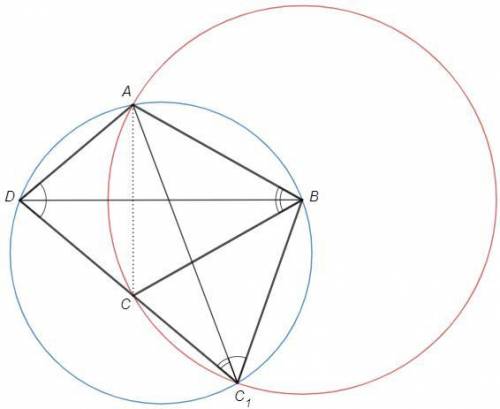
Точки A и С лежат на окружности с центром B.
Стороны угла ADC симметричны относительно биссектрисы DB.
DC пересекает окружность в двух точках (∠DAB не прямой - DA и DC не касательные).
В первом случае точка С симметрична точке A. Тогда DB - биссектриса △ABC, ∠ABC=60, △ABC - равнобедренный с углом 60 - равносторонний, ACB=60°
Во-втором случае (точка C1) докажем, что ABC1D - вписанный.
∠ABD =∠ABC/2 =∪AC/2 =∠AC1D
Отрезок AD виден из точек B и C1 под равным углом - A B C1 D на синей окружности. Тогда ∠AC1B=∠ADB=40°
1. Сторона треугольника a= 2Rcos30o.
2. 1) Знайдемо радіус вписаного кола у правильний трикутник:
2) Діагональ вписаного у коло квадрата рівна діаметру цього кола і дорівнює подвоєному радіусу:
3) Сторону квадрату знайдемо за т. Піфагора:
3.
4.В трапецию можно вписать окружность, если сумма противоположных сторон равна. то есть AD+BC=AB+CD
Опустим с вершины B трапеции на основание BK высоту BK, тогда
AK=AD-KD=28-21=7
Пусть высота трапеции BK=x, тогда
(AB)^2=(BK)^2+(AK)^2=x^2+7^2
AB=sqrt(x^2+7^2)
Так как
AD+BC=AB+CD, то
21+28=x+sqrt(x^2+7^2)
sqrt(x^2+7^2)=49-x
x^2+7^2=(49-x)^2
x^2+49=2401-98x+x^2
98x=2352
x=24, то есть высота трапеции равна 24
R=H/2
R=24/2=12 - радиус вписанной окружности