Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - ромб.
∠АВС - острый.
ВЕ и ВР - высоты, проведённые к сторонам ромба AD и CD соответственно.
∠ЕВР = 150°.
ВЕ = 6 см.
Найти:Р(ABCD) = ?
Решение:Рассмотрим четырёхугольник ВЕDP.
Сумма углов четырёхугольника равна 360°.
То есть -
∠Е+∠D+∠P+∠В = 360°
∠D = 360°-∠Е-∠Р-∠В
∠D = 360°-90°-90°-150°
∠D = 30°.
Рассмотрим соответственные ∠EAB и ∠D при АВ║CD (параллельны по определению ромба) и секущей ED.
∠EAB = ∠D = 30° (по свойству соответственных углов при параллельных прямых и секущей).
Рассмотрим прямоугольный ΔЕВА.
Против угла в 30° лежит катет, равный половине гипотенузы.
То есть -
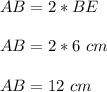
У ромба равны все стороны.
Следовательно -
Р(ABCD) = 4*АВ = 4*12 см = 48 см.
ответ: 48 см.
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2