26.
Объяснение:
Высоты треугольника пересекаются в одной точке, поэтому достаточно найти точку пересечения двух высот.
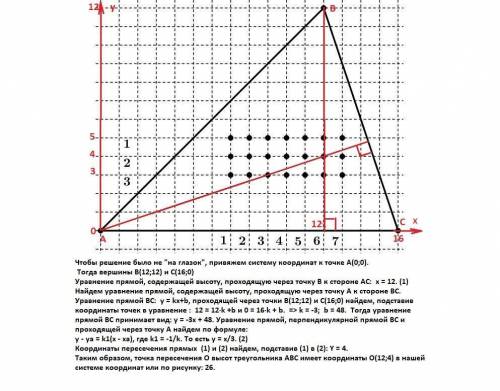
Чтобы решение было не "на глазок", привяжем систему координат к точке А(0;0). Тогда вершины В(12;12) и С(16;0)
Уравнение прямой, содержащей высоту, проходящую через точку В к стороне АС: x = 12. (1)
Найдем уравнение прямой, содержащей высоту, проходящую через точку А к стороне ВС.
Уравнение прямой ВС: y = kx+b, проходящей через точки В(12;12) и С(16;0) найдем, подставив координаты точек в уравнение : 12 = 12·k +b и 0 = 16·k + b. => k = -3; b = 48. Тогда уравнение прямой ВС принимает вид: y = -3x + 48. Уравнение прямой, перпендикулярной прямой ВС и проходящей через точку А найдем по формуле:
y - ya = k1(x - xa), где k1 = -1/k. То есть
y = x/3. (2)
Координаты пересечения прямых (1) и (2) найдем, подставив (1) в (2):
Y = 4.
Таким образом, точка пересечения О высот треугольника АВС имеет координаты О(12;4) в нашей системе координат или по рисунку: 26.
Нормальные векторы плоскостей, которые задают прямую а. равны:
n1 = (2; 1;-2) , n2 = (1; 1; 1).
Тогда направляющим вектором прямой а будет векторное произведение векторов n1 и n2.
a × b =
i j k
ax ay az
bx by bz
=
i j k
2 1 -2
1 1 1
= i (1·1 - (-2)·1) - j (2·1 - (-2)·1) + k (2·1 - 1·1) =
= i (1 + 2) - j (2 + 2) + k (2 - 1) = {3; -4; 1}.
Таким образом, вектор →
n = {3; -4; 1} будет нормальным вектором плоскости, перпендикулярной к прямой a.
Запишем искомое уравнение плоскости:
3(x − 2) + (-4)(y + 3) + 1(z − 5)
= 3x – 6 – 4y – 12 + z – 5 = 3x – 4y + z – 23 = 0.
ответ: 3x – 4y + z – 23 = 0.
Вектор ВА равен: ВА(1-(-2)=3;-2-1=-3;1-0=1) = (3;-3;1).
Вектор ДС равен: ДС(-2-Хд;-1-Уд;2-Zд).
Приравняем векторы:
3 = -2-Хд. Отсюда Хд = -2-3 = -5.
-3 = -1-Уд. Уд = -1+3 = 2.
1 = 2-Zд. Zд = 2-1 = 1.
2) Найти координаты вектора c=-a+(1/3)*b, если a(5;-4;2) и b(-3;3;0).
C=(-6;5;-2).
3) Обчислить скалярную сумму векторов AB и CD, если A(3;1;-4), B(-2,3,10), C(3,-1;2), D(6;-3;-2).
Скалярной суммы нет, есть просто сумма:
Вектор АВ(-2-3=-5; 3-1=2; 10+4=14) = (-5;2;14).
Вектор СД(6-3=3; -3+1=2; -2-2=-4) = (3;-2;-4).
Сумма равна (-5+3=-2; 2+(-2)=0; 14+(-4)=10) = (-2;0;10).
Скалярное произведение равно:
АВхСД =((-5)*3=-15)+(2*(-2)=-4)+(14*(-4)=-56) = -15-4-56 = -75.
4) Найти угол между векторами a(6;-2;-3) и b(5;0;0).
Косинус угла между векторами равен отношению их скалярного произведения к произведению их длин.
Этому косинусу соответствует угол 0,5411 радиан или 31,00272°.