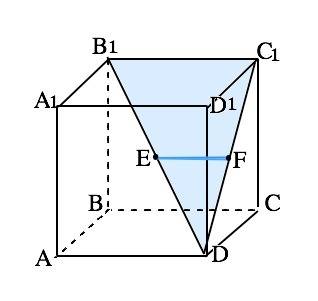
В ∆ В1DC1 отрезок EF соединяет середины сторон В1D и С1D, следовательно, EF- средняя линия и параллельна В1С1. Противоположные грани куба параллельны, противоположные стороны граней параллельны. ВС1 || А1D1, В1С1||ВС. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. ⇒ В1С1 параллельна плоскостям АBCD и ADD1A1.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо параллельна этой плоскости либо лежит в этой плоскости. EF параллельна В1С1,⇒ она параллельна АBCD и ADD1A1. EF параллельна В1С1, принадлежащей плоскости ВСС1В1 и А1В1С1D1, ⇒ прямая EF параллельна плоскостям четырех граней куба: АВСD. A1B1C1D1. AA1D1D, BB1C1C.
1) DX=(a+b)/2
DE=a
EX=DX-DE=(a+b)/2-a=a/2+b/2-a=b/2-a/2=(b-a)/2
при b больше a
2) CX=(a+b)/2
CE=b
EX=CX-EC=(a+b)/2-b=a/2+b/2-b=a/2-b/2=(a-b)/2
при a больше b
ответ расстояние от точки Е до середины отрезка DC EX=(/a-b/)/2, читать: "модуль разности (a-b) , деленный пополам"