Лучи om и on являются биссектрисами смежных углов aoc и boc соответственно. найдите угол между биссектрисами углов moc и noc.

👇

Ответ:

bbb87

02.04.2020

По моему MON!Так как On и OM делят AOC и BOC пополам
Лучи om и on являются биссектрисами смежных углов aoc и boc соответственно. найдите угол между биссе

Лучи om и on являются биссектрисами смежных углов aoc и boc соответственно. найдите угол между биссе

4,5(33 оценок)

Открыть все ответы

Ответ:

vika05lida811

02.04.2020

Давайте сначала рассмотрим две точки и посмотрим, при каких условиях прямая будет равноудалена от них (первый рисунок). Я утверждаю, что так будет, если или она параллельна отрезку, соединяющему эти точки, или проходит через середину этого отрезка.

Доказательство несложно: если прямая параллельна отрезку, то расстояние от неё до любой точки отрезка одинаково; в противном случае она пересекает прямую, содержащую отрезок. Но вне отрезка она пересечь не может - см. нижний рисунок, отрезки AHa, BHb не равны, поэтому она пересекает в некоторой точке C, принадлежащей отрезку (смотрим на верхний рисунок).
Опустим из точек перпендикуляры на прямую. Прямая равноудалена от точек, поэтому AHa = BHb. Кроме того, равны углы ACHa и BCHb - вертикальные. Отсюда прямоугольные треугольники ACHa и BCHb равны по катету и острому углу, и AC = CB.

Теперь возвращаемся к задаче. Будем думать, что нам даны вершины треугольника ABC. Искомая прямая не может быть параллельна более, чем одной стороне треугольника, две стороны она точно пересекает в середине. Значит, это средняя линия треугольника. Легко проверить, что средняя линия удовлетворяет условию.

ответ. (Второй рисунок) Искомая прямая - средняя линия треугольника, образованного данными точками. Задача имеет три решения - по числу средних линий.
Даны три точки, не лежащие на одной прямой. проведите прямую, равноудалённую от этих точек. сколько

Даны три точки, не лежащие на одной прямой. проведите прямую, равноудалённую от этих точек. сколько

4,5(32 оценок)

Ответ:

ЭймиКаннет

02.04.2020

1. Pabcd = 40 дм. 2. Sabc = 512 см².

Объяснение:

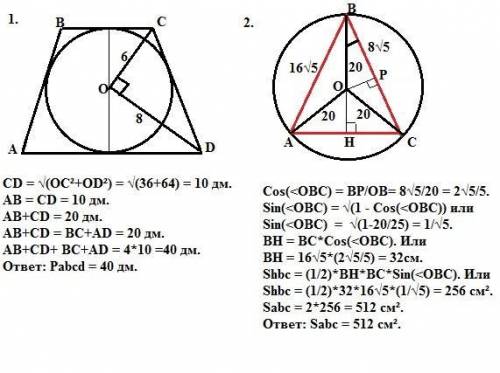
1. Свойство: Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. Следовательно, треугольник COD - прямоугольный, так как сумма его острых углов равна 90° (так как в трапеции <C + < D = 180°, => (1/2)*(<C+<D) =90°).

Тогда по Пифагору CD = √(OC²+OD²). Или

CD = √(36+64) = 10 дм. АВ = CD = 10 дм.

АВ+CD = 20 дм.

Свойство: Если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон. Следовательно, периметр нашей трапеции равен AB+CD+ BC+AD = 4*10 =40 дм.

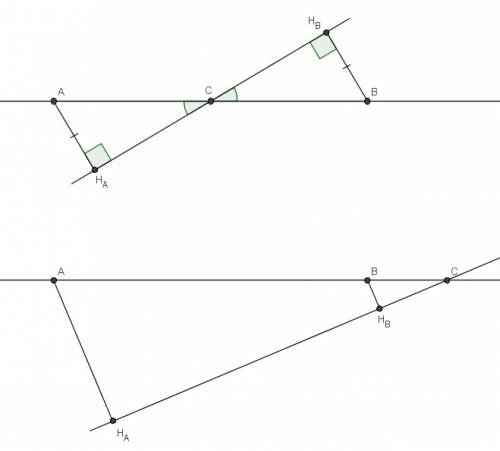
2. Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам. Тогда в прямоугольном треугольнике ОВР косинус угла ОВР равен отношению прилежащего катета ВР к гипотенузе ОВ.

ВР = 16√5/2 = 8√5см. ОВ = 20 см.

Cos(<OBC) = 8√5/20 = 2√5/5.

В прямоугольном треугольнике ВНС катет

ВН = ВС*Cos(<OBC) = 16√5*(2√5/5) = 32cм.

Площадь этого треугольника равна Shbc = (1/2)*BH*BC*Sin(<OBC).

Sin(<OBC) = √(1 - Cos(<OBC)) = √(1-20/25) = 1/√5. Тогда

Shbc = (1/2)*32*16√5*(1/√5) = 256 см². Это половина площади треугольника АВС (так как ВН - высота и медиана). Значит

Sabc = 2*256 = 512 см².