3) Дано уравнение 16x² + y² + 48x + 32 = 0.
Выделим полный квадрат по переменной х.
16(x² + 2*(3/2)x+(9/4)) – 16*(9/4) + y² + 32 = 0.
16(x + (3/2))²– 36 + y² + 32 = 0.
16(x + (3/2))² + y² = 4. Делим обе части на 4.
((x + (3/2))²/(1/4)) + (y²/4) = 1.
((x + (3/2))²/(1/2)²) + (y²/2²) = 1.
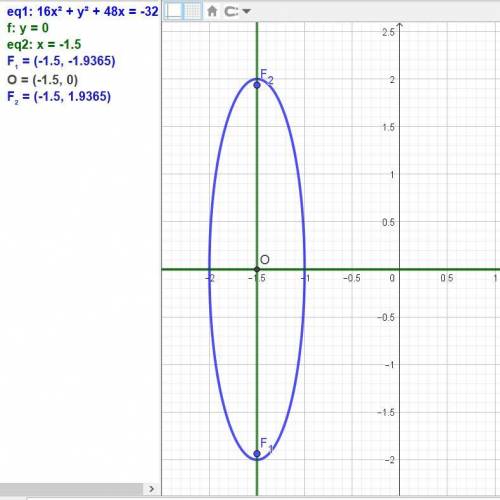
Получено каноническое уравнение эллипса с центром в точке О(-1,5; 0) и длинами полуосей: а = (1/2), b = 2.
Так как b > a, то главная ось параллельна оси Оу.
Расстояние от центра до фокуса с = √(b² - a²) = √(4 – (1/4)) = √15/2.
Координаты фокусов: F₁ = (-1,5; -√15/2), F2 = (-1,5; √15/2).
Координаты вершин: (-1,5; -2) и (-1,5; 2).
Дан трикутник з вершинами А(-1; √3), В(1; -√3), C(0,5; √3).
Координаты векторов сторон
АВ (c) BC (a) AС (b)
x y x y x y
2 -3,464 -0,5 3,4641 1,5 0
Длины сторон АВ (с) = √(4+ 12) = √16 = 4
BC (а) = √(0,25+1) = √12,25 = 3,5
AC (b) = √(2,25+0) = √2,25 = 1,5.
Углы по теореме косинусов
cos A = (b^2+c^2-a^2)/(2bc) = 6 /12 = 0,5
A = arccos 0,5 = 1,0472 радиан 60 градусов
cos B = (a^2+c^2-b^2)/(2ac) = 26/ 28 = 0,9286
B = arccos 0,9286 = 0,3803 радиан 21,7868 градуса
cos C = (a^2+b^2-c^2)/(2ab) = -1,5/ 10,5 = -0,1429
C = arccos -0,14286 = 1,71414 радиан 98,213 градуса
В равнобедренном треугольнике АВС (АВ=АС) угол А равен 100°, отрезок ВD- биссектриса треугольника. Докажите, что ВD+AD=BC ———————
Сделаем рисунок.
∠АВС=∠АСВ=(180°-100°):2=40°
Проведем биссектрису СМ и отрезок МD.
В ∆ АМС и ∆ АDВ стороны АВ=АС по условию.
Угол при А - общий, углы АВD=АСМ =40:2=20° как половины равных углов.
∆ АМС = ∆ АDВ по равной стороне и прилежащим к ней равным углам.
Следовательно, АМ=АD, и ∆ АМD - равнобедренный.
Углы треугольников АВС и АМD при их основаниях равны, они соответственные при пересечении двух прямых секущими, и поэтому МD||ВС (свойство), ⇒
∠ DМС=∠МСВ как накрестлежащие при параллельных прямых и секущей.
А т.к. СМ - биссектриса, то ∠ DСМ=∠ МСD
∆ МDС - равнобедренный, МD=DС.
Отложим на ВС отрезок ВК=ВD Соединим D и К.
∆ КВD - равнобедренный по построению.
Угол КВD=20°. следовательно, углы при КD=по 80°
Тогда угол СКD=100° как смежный углу DKB .
∠ КДС=180°-100°-40°=40° ⇒ ∆ СКD - равнобедренный. и равен треугольнику МАD по стороне и прилежащим к ней углам. КС=АD
ВС=ВК+КС, КС=АD, ⇒ ВD+АD=ВС, что и требовалось доказать.