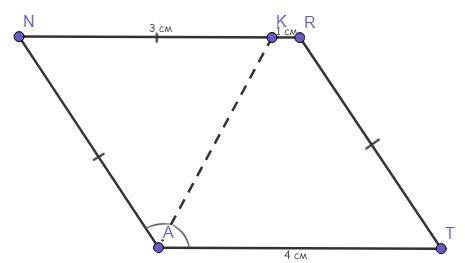
Четырёхугольник ANRT - параллелограмм.
АК - биссектриса ∠А.
NK = 3 cм.
KR = 1 см.
Найти :Р(ANRT) = ?
Решение :Биссектриса угла параллелограмма отсекает от параллелограмма равнобедренный треугольник (это не сложно доказать, если рассмотреть полученные накрест лежащие углы при параллельных прямых).Следовательно, ΔANK - равнобедренный (причём AN = NK = 3 см).
NR = NK + KR = 3 см + 1 см = 4 см.
Периметр параллелограмма равен удвоенной сумме его смежных сторон.Отсюда -
Р(ANRT) = 2*(AN + NR) = 2*(3 см + 4 см) = 2*7 см = 14 см.
ответ :14 см.
Определить боковую сторону равнобедренного треугольника , если синус угла(острого) при вершине равен 0,96, а радиус описанной около него окружности равен 12,5 см.
ответ: 20 см
Объяснение:
Обозначим данный треугольник АВС; АВ=ВС=х.
1)
По т.синусов найдем длину основания.
2R=AC/sin(ABC)
25=AC/0,96=>
AC=24 (см)
2)
a) Найдем косинус угла АВС:
cos²(ABC)=1-sin²(ABC)=0,0784 =>
cos(ABC)=0,28
б) По т.косинусов найдем длину боковой стороны.
АС²=АВ²+ВС²-2АВ•ВС•cos(ABC)
576=х²+х²-2х²•0,28
576=1,44х²
х²=400
х=√400=20(см)
Противоположные стороны параллелограмма равны и параллельны.
∠AKN = ∠KAT, как внутренние накрест лежащие углы при RN║AT и секущей AK.
∠KAT = ∠KAN, как углы при биссектрисе AK угла NAT.
Таким образом ∠AKN = ∠KAN. Значит, ΔNAK - равнобедренный (AK - основание), поэтому NA = KN = 3см, как боковые стороны.
RT = NA = 3см, как противоположные стороны параллелограмма ANRT.
RN = NK+KR = 3см+1см = 4см
TA = RN = 4см, как противоположные стороны параллелограмма ANRT.
P(ANRT) = AN+NR+RT+TA = 3см+4см+3см+4см = 14см
ответ: 14см.