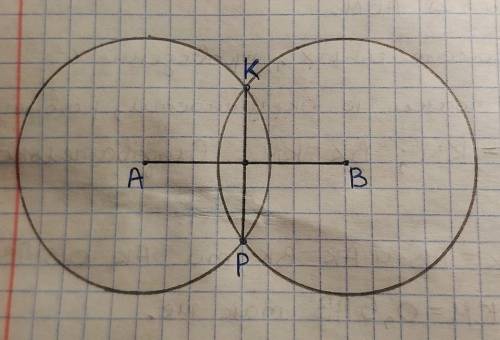
1. Поставить циркуль иглой в любой конец отрезка.
2. Развести циркуль, так чтобы расстояние между иглой и грифелем (то есть радиус будущей окружности) было не менее, чем половина данного отрезка или ровно половина отрезка (лучше взять больше. Например: равным с отрезок или даже больше чем отрезок).
3. Начертить окружность.
4. Поставить циркуль иглой в другой конец отрезка.
5. Развести циркуль, чтобы расстояние между иглой и грифелем (то есть радиус будущей окружности) был такой же, как в пункте 2 (менять расстояние нельзя!).
6. Начертить вторую окружность.
7. Соединить точки пересечения окружностей (на чертеже точки К и Р).
8. Найти точку пересечения изначально данного отрезка и проведенного отрезка (на чертеже отрезки КР и АВ, и точка О)
Данная точка и будет являться серединой данного отрезка.
Задание 6
Дано:
ΔADC - равнобедренный
BK = KD
AC = CD
∠BCK = 30°
Найти:
∠CBA - ?
ΔADC - равнобедренный (по рис.) ⇒ ∠B = ∠D (по свойству равнобедр. треуг.).
Отрезок CK - медина (делит противолежащую сторону на две равные) является высотой (по свойству равнобедр. треуг.) ⇒ ∠CKB = 90°.
∠CBK + ∠CKB + ∠BCK = 180° (по свойству треуг.)
∠CBK + 90° + 30° = 180°
∠CBK = 180° - (90° + 30°)
∠CBK = 60°
∠CBK и ∠CBA - смежные ⇒ ∠CBK + ∠CBA = 180°
60° + ∠CBA = 180°
∠CBA = 120°
ответ: ∠CBA = 120°.
Задание 7
Дано:
ΔCAD - равнобедренный
CA = DA
CB = BD
Найти:
∠CBA - ?
ΔCAD - равнобедр. (по рис.)
⇒ Отрезок BA - медианой (делит противолежащую сторону на две равные), является высотой (по свойству равнобедр. треуг.) и образует углы (∠CBA и ∠DBA) в 90°.
⇒ ∠CBA = 90°
ответ: ∠CBA = 90°.
Задание 8
Дано:
ΔDBK - равнобедр.
DM = MK
DB = BK
∠K = 70°
Найти:
∠CBA - ?
ΔDBE - равнобедр. (по рис.)
BM - медиана (делит противолежащую сторону на две равные)
⇒ BM - биссектриса и высота (по свойству равнобедр. треуг.)
⇒ ∠BME = 90°.
∠K + ∠BME + ∠MBE = 180° (по свойству треуг.)
⇒ 70° + 90° + ∠MBE = 180°
∠MBE = 180° - (70° + 90°)
∠MBE = 20°
Т.к. BM - биссектриса, то ∠DBE = 2∠MBE = 40°
∠DBE и ∠CBA - вертикальные
⇒ ∠DBE = ∠CBA = 40°
ответ: ∠CBA = 40°.
При пересечении, диагонали прямоугольника делятся пополам, а так как сами диагонали равны, то половины их тоже раны.
Треугольник, образованный меньшей стороной прямоугольника и половинками примыкающих к ней диагоналей - правильный, поскольку в нём между равными сторонами лежит угол 60°, то и остальные углы тоже 60°. Соответственно, меньшая сторона нашего прямоугольника равна половине его диагонали, то есть 14 см - это ответ.