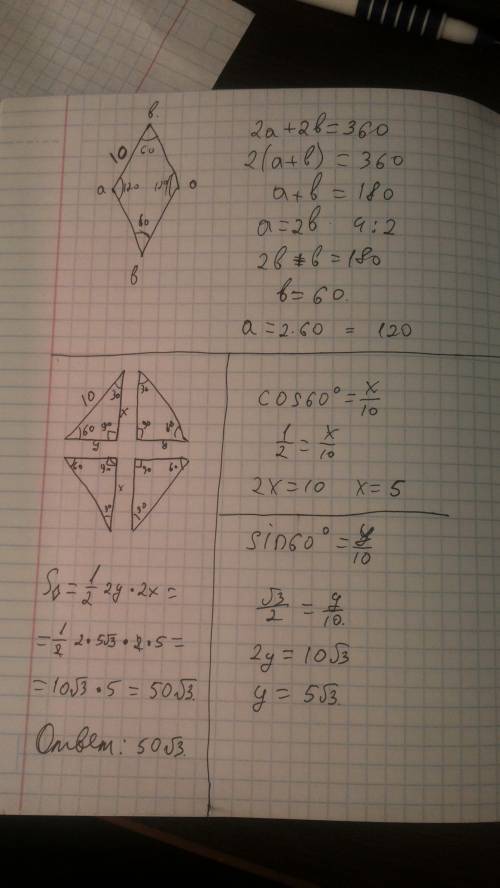
<BAC = 30° (150°).
Объяснение:
В прямоугольном треугольнике СЕА косинус угла А равен
CosA = AE/AC.
В прямоугольном треугольнике ADB косинус угла А равен
CosA = AD/AB.
Следовательно, АЕ/АС = AD/AB. => треугольник DAE подобен треугольнику АВС c коэффициентом подобия, равным CosA.
CosA = DE/BC = 3/2√3 = √3 /2.
ответ: угол А равен 30°. (Или 150° для тупоугольного треугольника с тупым углом А).
P.S. Насчет подобия - это теорема, которую, может быть, Вы не проходили. Она справедлива, естественно, для любых треугольников. Но для любознательных привожу все варианты.
1. Раз надо половину - проводим биссектрису :))) Получился египетский треугольник (5,12,13) (точнее, их получилось 2 :)) Отсюда, если угол Ф, то
sin(Ф/2) = 5/13; cos(Ф/2) = 12/13; tg(Ф/2) = 5/12
2. Опускаем высоты из В и С на AD, и видим по бокам 2 РАВНОБЕРЕННЫХ прямоугольных треугольника - у них гипотенузы 2, а катеты, которые - куски AD, равны корень(2) :). То есть углы 45 и, само собой ,135 градусов.
3. делаем то же самое, но уже только с одной стороны, потому что мы уже знаем (в предыдущем пункте считали :)), что отрезок от D до основания высоты из С на AD, равен полуразности оснований, то есть, в данном случае, (18-12)/2 = 3. Поэтому высота равна 3*(корень(3)/3) = корень(3)
а диагональ находится из треугольника, образованного ДРУГОЙ высотой - из В на AD и отрезком 18 - 3 = 15 (между прочим, это равно средней линии :).
d = корень(15^2 + (корень(3))^2) = 2*корень(57)