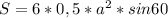Найти стороны параллелограмма авсd, если его периметр равен 60 см, а сторона ав больше вс в 2 раза

👇

Увидеть ответ

Ответ:

1Серж1111111111

07.10.2020

Р=2(АВ+ВС)
АВ=2ВС
60=2(2ВС+ВС)
40=3ВС
ВС=13 ⅓
АВ=26 ⅔

4,5(42 оценок)

Открыть все ответы

Ответ:

karachevamaria4

07.10.2020

АВСЕ - пирамида с вершиной Е.
В основании лежит правильный тр-ник, для которого радиус описанной окружности в два раза больше радиуса описанной окружности. r=R/2.
ОК=ОВ/2=2а/2=а.
ЕК - апофема на сторону АС.
В тр-ке ЕКО ЕК²=ЕО²+ОК²=3а²+а²=4а²,
ЕК=2а - апофема.
б) ЕК/ОК=2а/а=2. В прямоугольном треугольнике ЕОК гипотенуза ЕК вдвое больше катета ОК, значит ∠КЕО=30°, следовательно ∠ЕКО=60° - угол между боковой гранью и основанием.
в) Площадь боковой поверхности: Sб=Р·l/2, где Р - периметр основания, l - апофема.
R=AB/√3 ⇒ AB=R√3=2a√3.
P=3AB=6a√3.
Sб=6a√3·2a/2=6a²√3 (ед²).
Высота правильной треугольной пирамиды равна а(корень из 3), радиус окружности, описанной около ее о

Высота правильной треугольной пирамиды равна а(корень из 3), радиус окружности, описанной около ее о

4,4(79 оценок)

Ответ:

Аришка8668

07.10.2020

Правильный шестиугольник можно разделить на 6 правильных треугольников, поэтому площадь шестиугольника будет равна

$S=6*0,5*a^{2}*sin60$ , где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 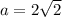$a=2 \sqrt{2}$ . Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60= 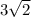$3\sqrt{2}$ . Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.

ответ: 18.

4,4(73 оценок)

Это интересно:

Дом-и-сад

31.07.2022

Как покрасить ткань чаем: возможности и результаты...

Стиль-и-уход-за-собой

07.09.2020

Как подчеркнуть изгибы своего тела: советы от профессионалов...

Дом-и-сад

27.07.2022

Как выращивать мяту: советы от опытных садоводов...

Здоровье