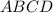 , стороны
, стороны 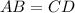 , опустим высоту
, опустим высоту 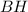 .
.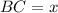 , тогда
, тогда 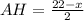
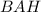 .
. 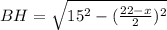
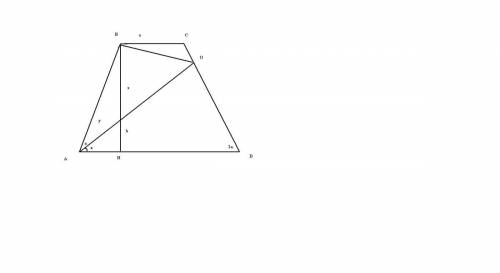
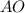 является биссектрисой треугольник
является биссектрисой треугольник 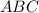 , то по формуле она равна
, то по формуле она равна 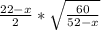
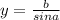
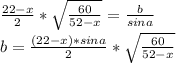
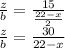
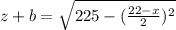
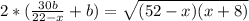
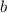
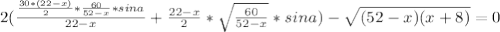
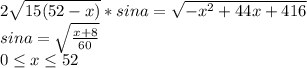
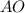 это сама биссектриса тогда , угол
это сама биссектриса тогда , угол 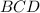 равен
равен 
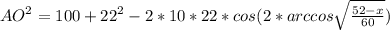
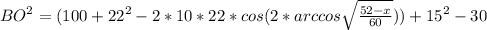 *
*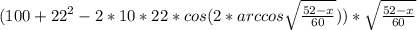
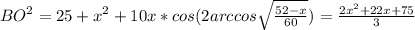
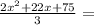
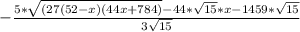
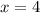
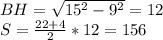
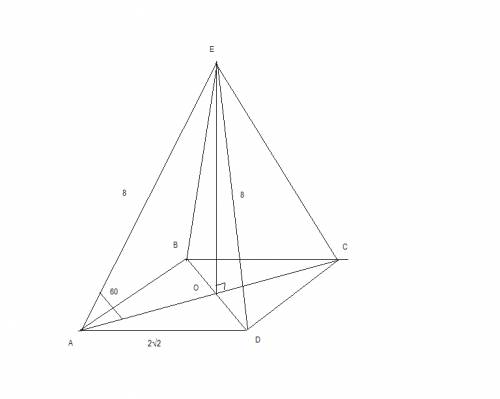
Боковое ребро правильной четырёхугольной пирамиды равняеться 8 см. и образует с площадью основания угол 60 градусов.Найти площадь боковой поверхности приамиды Sбок
правильная четырёхугольная пирамида -значит ABCD -квадрат
проекция AO бокового ребра AЕ на плоскость основания -это половина диагонали квадрата
АО=AЕ*cos60=8*1/2=4
треугольник АОD- прямоугольный АО=OD=4
гипотенуза AD= √(AO^2+OD^2)= √(4^2+4^2)= 2√2
рассмотрим треугольник AЕD
полупериметр р=(8+8+2√2)/2=8+√2
тогда по теореме Герона площадь треугольника
S(AЕD )= √[(8+√2)( 8+√2-8)( 8+√2-8)( 8+√2-2√2)]=2√31
площадь боковой поверхности приамиды Sбок= 4*S= 4*2√31 =8√31
ответ Sбок= 8√31