DA = 5см
Объяснение:
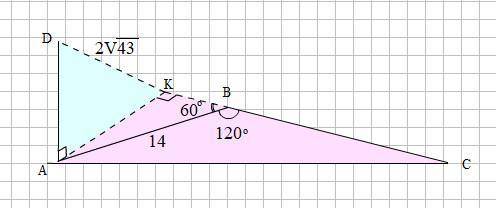
Смотри рисунок на прикреплённом фото.
Дано, что DA ⊥ плоскости ΔАВС.
Делаем дополнительное построение: из точки А опускаем перпендикуляр АК на продолжение стороны ВС. (АК⊥ВС). Точку D соединяем с точкой К, образовав пл-ть ADK. Докажем, что DK - расстояние от точки D до прямой ВС, то есть DK⊥ BC.
Пл-ть ADK ⊥ пл-ти АВС, так как прямая AD, принадлежащая пл-ти АDK, перпендикулярна пл-ти АВС (AD∈ ADK и AD⊥пл-ти АВС ⇒ пл-ть АDK ⊥ пл-ти ABС).
Далее. Поскольку прямая ВС ⊥ АК (линии пересечения пл-тей АВС и АDK), то она перпендикулярна пл-ти ADK.
И поскольку ВС ⊥ пл-ти ADK, то она перпендикулярна каждой прямой пл-ти ADK, проходящей через точку пересечения К. Таким образом, DK⊥BC и является расстоянием от точки D до прямой ВС. DK = 2√43, по условию.
∠АВК и ∠АВС смежные углы, поэтому
∠АВК = 180° - ∠АВС = 180° - 120° = 60°.
АК = АВ·sin 60° = 14 · 0.5√3 = 7√3 (cм).
По теореме Пифагора DK² = AK² + DA², откуда
DA = √(DK² - AK²) = √(4 · 43 - 49 · 3) = √172 - 147 = √25 = 5(см)
Так как диагональ ромба является биссектрисой угла, а угол между диагональю и стороной равен 45 градусам,то весь угол является биссектрисой равен двум углам,т.е 45*2=90, а так как в ромбе две пары равных углов и сумма одной из этой пары равна 90+90=180, а сумма углов в ромбе равняется 360 градусам,то сумма углов другой пары равняется 360-180=180, а так как в этой паре два равных угла ,то каждый угол равен 90 градусов.