Объяснение: задание 2 практическое. Нужно начертить в тетради отрезок любой длины, отмерять циркулем эту длину и провести окружность.
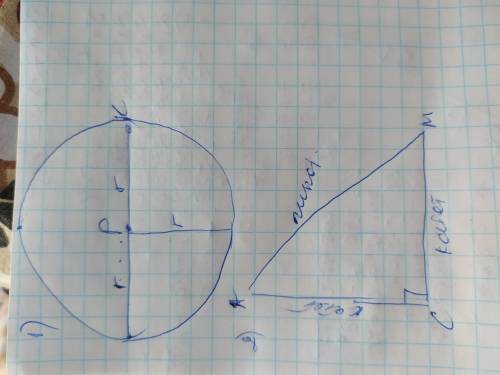
ЗАДАНИЕ 3
АС и ВС - катеты, АМ- гипотенуза
ЗАДАНИЕ 4
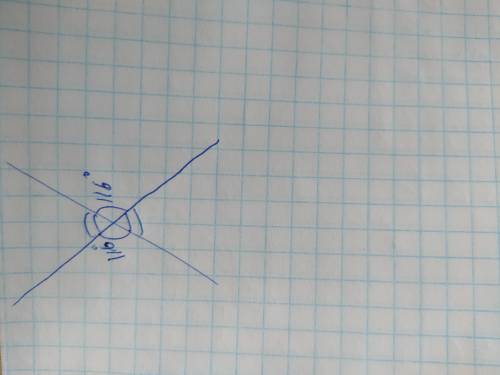
Сумма углов при пересечении прямых составляет 360°, причём противоположные углы между прямыми равны. Найдём сумму двух других углов между прямыми:
360-116×2=360-232=128°. Так как эти два угла равны то каждый из них=
=128÷2=64°
ответ: каждый и 2-х остальных углов составляет 64°
ЗАДАНИЕ 5
Если треугольник равнобедренный то две его боковые стороны будут по 8см каждая. Зная периметр найдём основание треугольника:
26-2×8=26-16=10см
ответ: основание треугольника=10см
ЗАДАНИЕ 6
Рассмотрим ∆АВС и ∆ДСВ. У них:
АВ=СД по условиям, угол АВС= углу ДСВ, по условиям, сторона ВС -общая. Эти треугольники равны по первому признаку: по двум сторонам и углу между ними.
Что и требовалось доказать
ЗАДАНИЕ 7
Пусть третий угол=х, а второй угол=х+16. Зная третий угол и что сумма углов треугольника составляет 180°, составим уравнение:
х+х+16+36=180
2х+52=180
2х=180-52
2х=128
х=128÷2
х=64
Итак 3-й угол = 64°, тогда второй угол=64+16=80°
ответ: угол2=80°; угол3=64°
Объяснение:
Мы знаем что угол при основании равен 60*. Проводя высоту мы получаем прямоугольный треугольник, и отсюда следует, что второй угол равен 30°. Тогда часть большего основания, лежащего напротив этого угла, равна её половине. И с другой стороны трапеции, так как она равнобедренная, то будет то же самое.
Теперь по теореме Пифагора находим высоту:
h = √(12²-6²) = √(144-36) = √108 = 6√3. Теперь найдём всю длину большего основания:
Две части мы нашли (они равны по 6 см), а третья часть равна меньшему основанию, большее основание равно 6+6+24=36.
Находим площадь по формуле S=1/2(a+b)*h
S=1/2(24+36)*6√3=30*6√3 =180√3.
ответ: 20 см, 33 см, 33 см.
Объяснение:
Так как два внешних угла треугольника при разных вершинах равны, следовательно, треугольник ABC равнобедренный.
Если AC = 20 см, то остальные стороны по (86 − 20) : 2 = 33 см.
Если AB = BC = 20 см, то основание равно 86 − 2 · 20 = 46 см. Но такого треугольника не может существовать. Значит, второе предположение неверно.