У параллелограмма ABCD проведена высота ВМ к стороне AD. Найдите площадь этого параллелограмма, если ВС = 8 см, ВМ = 5 см.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
Дано:Четырёхугольник ABCD — параллелограмм.
ВМ — высота, опущенная на сторону AD = 5 см.
ВС = 8 см.
Найти:S(ABCD) = ?
Решение:▸Противоположные стороны параллелограмма равны◂
AD и ВС — противоположные стороны.
Следовательно, по выше сказанному —
AD = ВС = 8 см.
▸Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону◂
Следовательно —
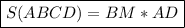
Подставим в формулу известные нам значения в формулу —
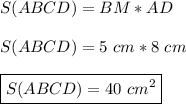ответ: 40 см².
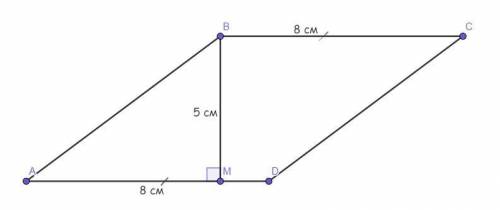
Поскольку AM перпендикулярна пллоскости квадрата, то она перпендикулярна любой прямой, лежащей в этой плоскости. В частности, AM перпендикулярна сторонам квадрата.
Расстоянием от точки M до вершины B есть отрезок MB. Рассмотрим прямоугольный ΔAMB(<MAB = 90° - по сказанному выше). AB = BC = 12 как стороны квадрата, AM = 5. По теореме Пифагора,
MB = √(AM² + AB²) = √(144+25) = √169 = 13. Итак, расстояние от точки M до вершины квадрата B равно 13 см.
Расстояние от точки M до вершины A есть отрезок MA и равно 5 см.
Найдём расстояние от точки M до вершины C(отрезок MC). Для этого проведём диагональ AC квадрата. Тогда по определению, MA перпендикулярна AC, то есть <MAC = 90°. Рассмотрим прямоугольный треугольник MAC, где AC - диагональ квадрата. MA = 5 см. Диагональ квадрата вычисляется по формуле AC = a√2, где a - длина стороны квадрата. AC = 12√2 см. по теореме Пифагора,
MC = √(MA² + AC²) = √(25 + 288) = √313 см - это расстояние от точки M до вершины C.
Ну и аналогично находим расстояние от точки Mдо вершины D. Для этого надо рассмотреть прямоугольный треугольник MAD и по теореме Пифагора найти гипотенузу MD. этот отрезок и является расстоянием от точки M до врешины D. Задача решена.
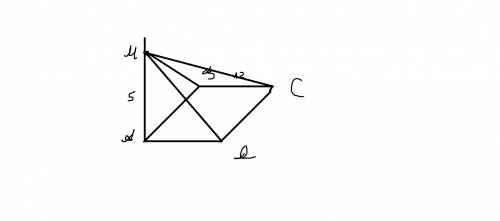
2Р - Р/2 = 121, откуда Р = 80 2/3.
ответ: 80 2/3