угол MBC = 30°
угол ВCA = 60
Объяснение:
Дано:
АВС - треугольник
АМ = СМ
уг. АВС = 60°
уг. ВМА = 90°
-------------
Найти
уг. МВС - ?
уг. ВСА - ?
Решение
угол ВМА = 90° => уг. ВМС = 90°
т.е. ВМ | АС, а значит,
ВМ - высота, проведенная из вершины В на АС.
Также АМ = МС, а значит
ВМ - медиана, проведенная из вершины В на АС.
Если медиана треугольника является его высотой, то этот треугольник - равнобедренный.
ВМ - высота и медиана ∆АВС, =>
=> ∆АВС - равнобедренный, основание АС =>
=> ВМ - также является биссектрисой ∆АВС, т.е.
уг. АВМ = уг. СВМ
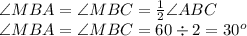
Так, как ∆АВС - равнобедренный, с основанием АС, то углы при основании - равны друг другу
уг. ВАС = уг. АСВ
и равны
угол ВАС = угол ВСА = 1/2 • (180 - угол АВС)
угол ВАС = угол ВСА = 1/2 • (180 - 60) = 60°
а значит ∆АВС - равносторонний.
угол MBC = 30°
угол ВCA = 60°
Доказательство.
Стороны равны - гипотенузы треугольников с равными катетами.
Вх-Ах=6-3 = 3 и Сх-Рх= 9-6 = 3
Ву-Ау= 6-4 = 2 и Су-Ру= 4-2 = 2.
Стороны параллельны- наклон отрезков одинаков.
k1 = ΔY/ΔX = (By-Ay)/(Bx-Ax) = 2/3 - наклон отрезка ВА.
k2 = (Cy-Py)/(Cx-Px) = 2/3 - наклон отрезка СР.
Аналогично для другой пары отрезков.
Настоящий параллелограмм и настоящий ромб.
ЧТД - что и требовалось доказать.