Т.к. КМ=МN, то треугольник равнобедренный, следовательно угол MKN= углу MNK( по свойству равнобердренного треугольника). Угол KMN= 180' - (MKN+MNK)
cos∠B = 0
cos∠A = 0,6
cos∠C = 0,8
Объяснение:
Найдем длины сторон треугольника по формуле расстояния между точками:
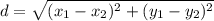
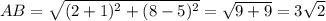
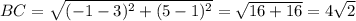

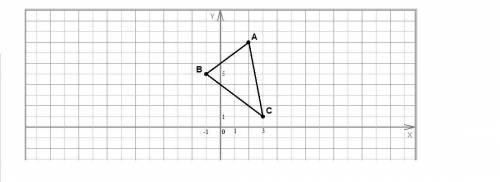
Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:
AC² = AB² + BC²
(5√2)² = (3√2)² + (4√2)²
50 = 18 + 32
50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус прямого угла равен нулю.
cos∠B = 0
cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6
cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8
Из прямоугольного треугольника ABD
AD^2=AB^2+BD^2=9+16=25
AD=5
Площадь основания равна 2*площадь ABD=2*(3*4/2)=3*4=12
AD параллельно BC, следовательно параллельно B1C1, поэтому AD принадлежит плоскости AB1C1, и это прямая пересечения плоскости основания с плоскостью AB1C1
Пусть BE высота в треугольнике ABD
Тогда угол B1EB это угол между плоскостью основания и плоскостью AB1C1, так как BE перпендикулярно AD, B1E перпендикулярно AD по теореме о трёх перпендикулярах.
Треугольник B1EB -- прямоугольный треугольник с углом 45 градусов, а следовательно, равнобедренный прямоугольный треугольник, поэтому B1B=BE
Чтобы найти высоту BE выразим площадь треугольника ABD двумя
площадь ABD = AB*BD/2 = AD*BE/2, отсюда
BE=AB*BD/AD=3*4/5=12/5=2,4
Площадь полной поверхности равна
2*площадь основания+площадь боковой поверхности
площадь боковой поверхности = периметр основания умножить на высоту
периметр основания = AB+BC+CD+AD=3+5+3+5=16
тогда площадь боковой поверхности 16*2,4=38,4
площадь полной поверхности
2*12+38,4=24+38,4=62,4
КМ=МN (10=10)
МN<KN (10<15)
KM<KN (10<15)