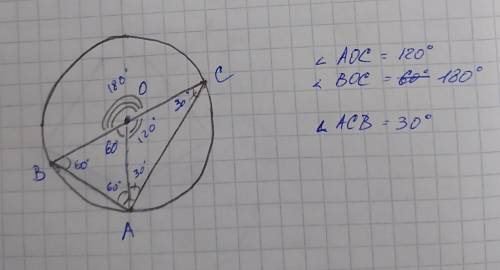
2. ∠AOC = 120°; ∠BOC = 180°; ∠ACB = 30°
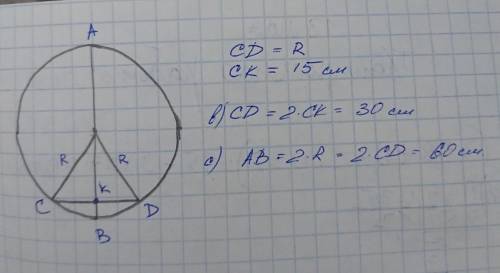
3. CD = 30 см; AB = 60 см
Объяснение:
2. Упростим соотношение дуг: 3:9:6 <=> 1:3:2 <=> AB, BC, AC
Найдём их градусную меру:
AB + BC + AC = x + 3x + 2x = 360°
6x = 360°
x = 60°
AB - 60°
BC - 180°
AC - 120°
Отразим это на рисунке.
Легко видеть, что
∠AOC = 120°; ∠BOC = 180°
На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
3. Рисунок и решение на фото.
1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
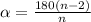
Найдем при каком n угол будет равен 160°:
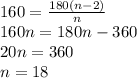
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
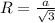
Подставим заданное значение стороны:
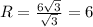
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
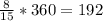 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см