Объяснение:
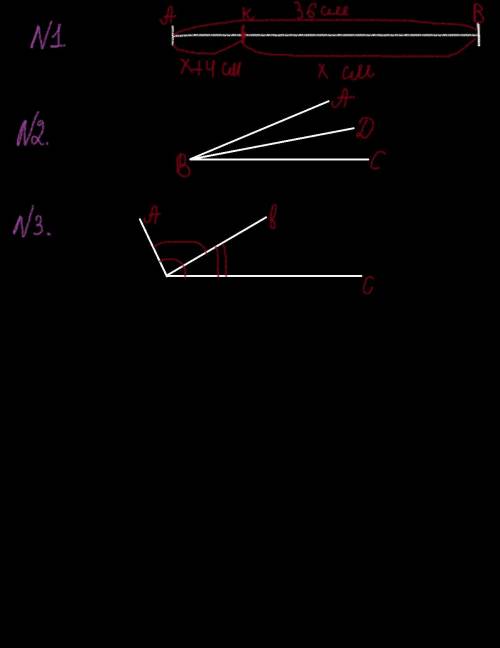
Задача №1.
Давайте примем отрезок BK за x. Тогда отрезок AK будет равен x + 4 cм (потому что AK больше BK на 4 см).
Составляем уравнение:
x + x + 4 = 36
2x = 36 -4
2x = 32
x = 16 см - отрезок BK (потому что BK мы приняли за x).
Теперь можем найти отрезок AK. Из условия задачи известно, что AK больше BK на 4 см.
Следовательно:
AK = BK + 4 cм = 16 см + 4 см = 20 см.
Задача решена.
Задача №2.
Углы ABC и DBC являются смежными, потому что лежат на одной прямой, а две другие прямые являются дополнительными полупрямыми этих углов.
Имеем:
1) ∠ABC + ∠DBC = 180° (по свойству смежных углов)
Чтобы найти эти углы, надо составить уравнение, которое решало бы эту задачу.
Пусть x - это ∠DBC, тогда ∠ABC будет равен x + 38° (угол ABC больше ABD на 38°).
Имеем:
x + x + 38° = 180°
2x = 142
x = 71° - ∠DBC (так как угол DBC мы взяли за x).
Теперь найдем угол ABC:
2) ∠ABC = 71° + 38° = 109°
Так как эти углы делит пополам биссектриса, то углы, образованные при пересечении биссектрисы будут равны.
Чтобы их найти, мы 109 разделим на 2.
3) ∠ADB = 109° : 2 = 54,5°
Задача решена.
Задача №3.
Когда биссектриса делит угол пополам, образовываются другие углы, градусная мера которых будет в два раза меньше.
1) 150° : 2 = 75° - углы, образованные при пересечении луча b.
2) 75 + 40 = 115°
A)8
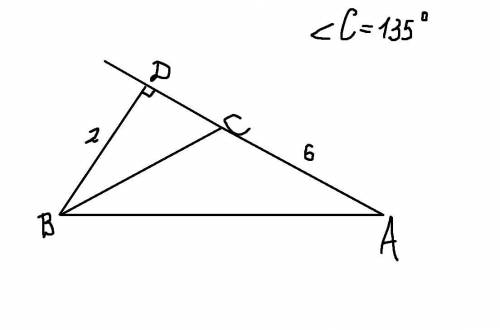
Объяснение:
Сначала нужно нарисовать рисунок(см. рисунок). Как мы видим: треугольник ABD - прямоугольный с гипотенузой АВ. А это значит, что для нахождения его площади необходимо знать два его катета, при чём один из которых нам уже известен. Теперь вся задача сводится к тому, чтобы найти отрезок DC. Поскольку угол ВСА равен 135°, то смежный с ним угол BCD будет равен 180°-135°=45°. Значит прямоугольный треугольник BCD - равнобедренный. А это значит, что BD=DC=2. Тогдда AD = 6+2=8.
Теперь найдём площадь треугольника ABD:
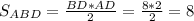
∠(AB,CM) = 60°
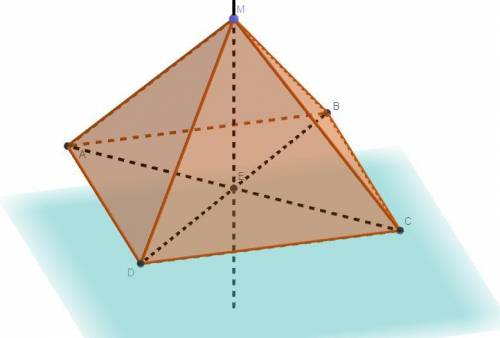
Объяснение:
Дано: MABCD - правильная четырехугольная пирамида, MD = DC
Найти: ∠(AB,CM) - ?
Решение: По определению пирамиду называют правильной если, её основание правильный многоугольник, а высота пирамиды является центром этого многоугольника. Правильным четырехугольником является квадрат. По определению угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым, тогда так как ABCD - квадрат, то AB ║ DC, следовательно ∠(AB,CM) = ∠(MD,DC) = ∠MDC .Пусть диагонали квадрата пересекаются, в точке E. Точка пересечения диагоналей квадрата является центром квадрата. Треугольник ΔMED и ΔMEC - прямоугольны так как ME - высота пирамиды, следовательно ΔMED = ΔMEC по двум катетам так как ME - общая и делит диагонали на четыре равны отрезка по свойству квадрата, тогда DE = EC. ΔMED = ΔMEC ⇒ MD = MC, а так как по условию MD = DC, то MD = MC = DC и треугольник ΔMDC - правильный, тогда по свойству правильного треугольника каждый его угол 60° и ∠MDC = ∠(AB,CM) = ∠(MD,DC) = 60°.
BK-16см
Не факт что правильно