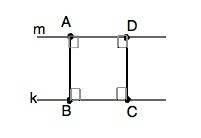
Дано :
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
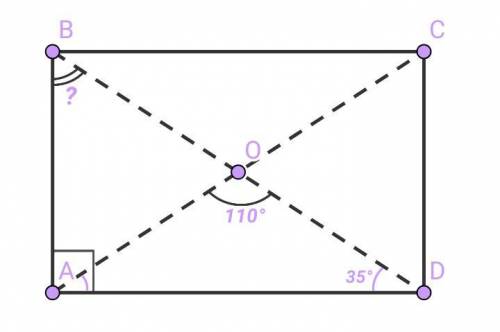
Расстояние между двумя параллельными прямыми есть длина перпендикуляра, опущенного из некой точки одной прямой на другую.
. Пусть даны параллельные прямые m и k
Возьмём на прямой m произвольную точку А и проведем через неё перпендикуляр до пересечения с прямой k в точке В
Так как если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой, то углы, образованные отрезком АВ - и прямыми m и k - прямые.
Таким же образом выберем на некотором расстоянии от т.А точку D и проведем через неё перпендикуляр DC, который образует с прямыми m и k прямые углы.
Четырёхугольник АВСD- прямоугольник (все углы прямые). Так как в прямоугольнике противоположные стороны равны, АВ=СD, т.е точки А и D на прямой m равноудалены от прямой k. =>
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
-------------
Существуют и другие доказательства. Попробуйте найти их самостоятельно.