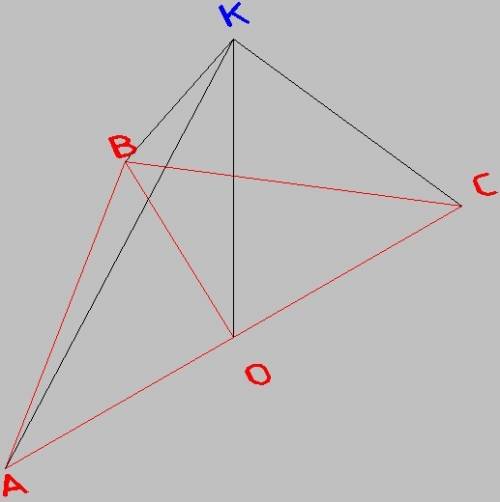
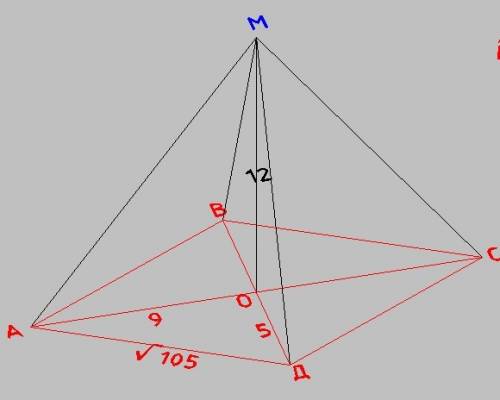
ответ: 80 см²
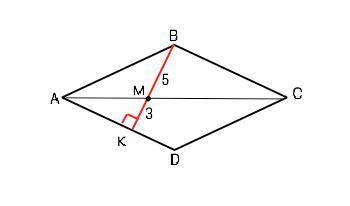
Объяснение: Диагонали ромба - биссектрисы его углов. В прямоугольном треугольнике АВК отношение гипотенузы АВ к катету ВК равно отношению отрезков. на которые биссектриса угла А делит высоту ВК: АВ:АК=5:3 - это отношение гипотенузы и катета «египетского» треугольника. Тогда ВК:АВ=4:5, Т.к. ВК=3+5=8, АВ=AD=10 см. Ѕ=ВК•AD=8˙10=80 см²
Или:
В ∆ АВК биссектриса АМ делит сторону ВК в отношении сторон, между которыми она проведена. Т.е. АВ:АК=ВМ:МК. Примем коэффициент отношения сторон равным а. Тогда АК=3а, АВ=5а.
По т.Пифагора АВ²-АК²=ВК².
ВК=ВМ+МК=5+3=8⇒
25а²-9а²=64
16а²=64, а*=4, а=√4=2
Сторона ромба =2•5=10
Площадь ромба равна произведению высоты на сторону.
Ѕ=АD•АК=10•8=80 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам, значит, треугольник ВОС равнобедренный, а у него углы при основании равны, т.е. угол ВСО=ОВС=54 град
Теперь смотри треугольник ВОС, два угла узнали. находим угол ВОС=180-(54+54)=72 град
Угол ВОС=углу АОД=72 град как вертикальные
Угол ВОА=180-72=108 град (развернутый угол =180 вычитаешь известный угол в 76 град,
второй или можешь рассмотреть треугольник АВО и он равнобедренный,т.е. углы ОВА=ВАО=36 град, находим угол АОВ=180-(36+36)= 108град
угол СОД=углу СОД=108 град
ответ: угол ВОС=ВОД=76 град
угол АОВ=СОД=108 град
Удачи!