
Отрезки касательных, проведенных к окружности из одной точки, – от данной точки до точек касания равны (свойство),
Радиус окружности, проведенный к точке касания, перпендикулярен касательной.
Сумма углов четырехугольника 360°
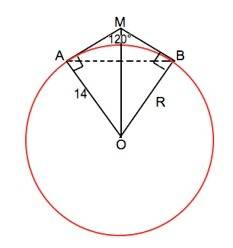
А и В - точки касания.
Следовательно, центральный угол АОВ, образованный радиусами ОА и ОВ, равен 360°-2•90° -120°=60°
Треугольники МАО и МВО равны по трем сторонам ( равные отрезки касательных и радиусы - катеты, МО - общая гипотенуза). ⇒
угол МОА=МОВ=60:2=30°
ОМ=R:cos30°=2R:√3=28:√3 см
Δ
Δ
Медианы треугольника пересекаются в одной точке и делятся в этой точке в отношении 2:1 (считая от вершины)
Δ
по теореме Пифагора найдем OA:
ответ: 4 см