Средняя линия треугольника параллельна стороне треугольника и равна ее половине . В условии не сказано, параллельно какой из сторон проведена средняя линия MN, поэтому может быть два варианта решения.
1 вариант:
MN параллельна основанию RS, RF=SF, RS+2*RF=30 (дано). Тогда
RS=8, а RF=(30-8):2=11.
2 вариант:
MN параллельна боковой стороне RF. Тогда
RF=SF=8, а RS=30-2*8=14.
Оба варианта удовлетворяют условию существования треугольника (теорема о неравенстве), так как большая сторона меньше суммы двух других сторон.
Объяснение:
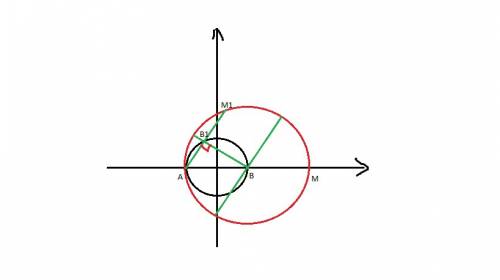
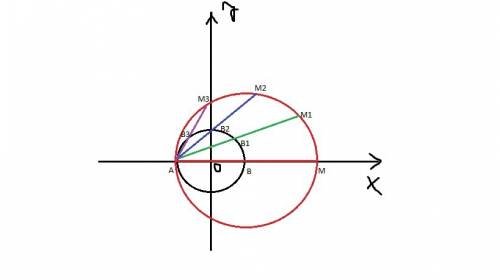
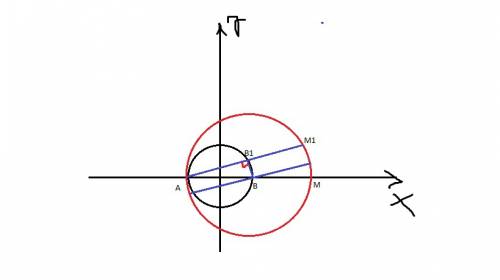
2. Треугольник AOD - прямоугольный, катет, лежащий против угла в 30 градусов равен половине гипотенузы, т.е. AO=½AD=11.
3. AD параллельна BC (как основания трапеции), при секущей OD угол OCB = угол ODA =30.
4. Треугольник BOC - прямоугольный, BO=½BC=5.
5. AB=AO-BO=11-5=6 см.