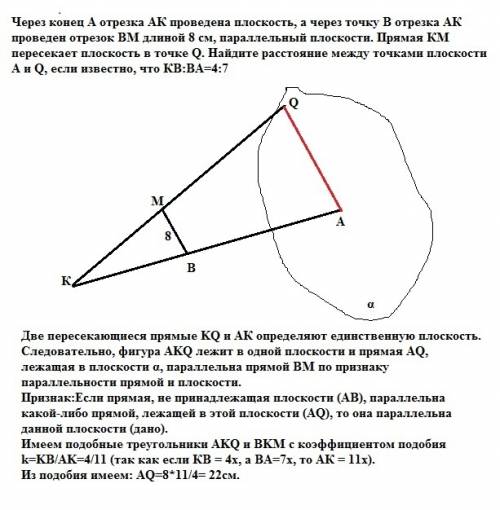
Две пересекающиеся прямые KQ и АК определяют единственную плоскость. Следовательно, фигура AKQ лежит в одной плоскости и прямая AQ, лежащая в плоскости α, параллельна прямой ВМ по признаку параллельности прямой и плоскости.
Признак:Если прямая, не принадлежащая плоскости (AB), параллельна какой-либо прямой, лежащей в этой плоскости (AQ), то она параллельна данной плоскости (дано).
Имеем подобные треугольники AKQ и BKM с коэффициентом подобия k=KB/AK=4/11 (так как если КВ = 4х, а ВА=7х, то АК = 11х).
Из подобия имеем: AQ=8*11/4= 22см. Это ответ.
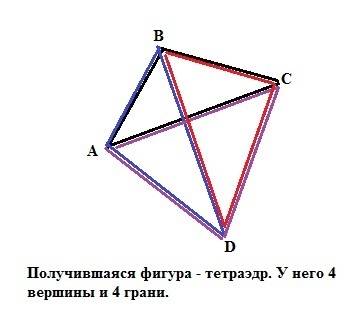
Через три точки можно провести плоскость и при том только одну. Хначит нам надо найти число сочетаний из 4 по 3 по известной формуле: 4!/((4-3)!*3! = 4. Но если эта формула нам не известна, то найти количество плоскостей можно простым перебором: пусть нам даны четыре точки: А,В,С и D. Тогда плоскости:
АВС, АВD, ADC и BCD (любые другие комбинации точек будут повторять уже имеющиеся, изменится лиш порядок следования букв в обозначениях плоскостей, например ВСА и АВС, а это одна и та же плоскость.
Получившаяся фигура - тетраэдр. У него 4 вершины (точки) и 4 грани (плоскости).
ответ: 4.
Пусть 1 и 3 - вертикальные углы. Так как сумма вертикальных углов 200, то 200:2=100 (потому что вертикальные углы равны) Углы 1 и 3 образуют с углами 2 и 4 смежные углы.
Т.е 1+2=180 градусов, 3+4=180 градусов. Значит, 180 - 100= 80 градусов. Углы 2 и 4 - 80 градусов. ответ: 80,80,100,100.
Можно и так было сделать, разницы нет. 1 и 3 - 200 градусов в сумме. А сумма всех четырех углов - 360. 360-200=160 градусов - сумма углов 2 и 4 (они то же вертикальные)
160:2=80
200:2=100 ответ: 80,80,100,100