а) Опустим высоту АН из вершины угла, и рассмотрим получившийся прямоугольный треугольник АВН,
{< - угол}
<Н=90°, по определению прямоугольного треугольника, зная сумму всех углов этого треугольника, найдем <ВАН
<ВАН=90°-60°=30°
Против угла в 30° лежит катет равный половине гипотенузы, а значит ВН=0,5*3=1,5
Найдем АН по теореме Пифагора
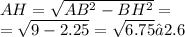
Найдем НС, зная ВН и ВС,

Рассмотрим треугольник АСН, прямоугольный,
Отсюда,
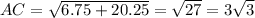
б) Периметр треугольника равен сумме сторон,
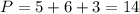
в)Площадь треугольника равна половине произведения АВ на НС и на SinB
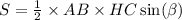
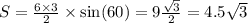
или
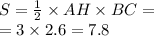
г) Радиус окружности можно вывести из формулы
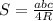
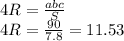

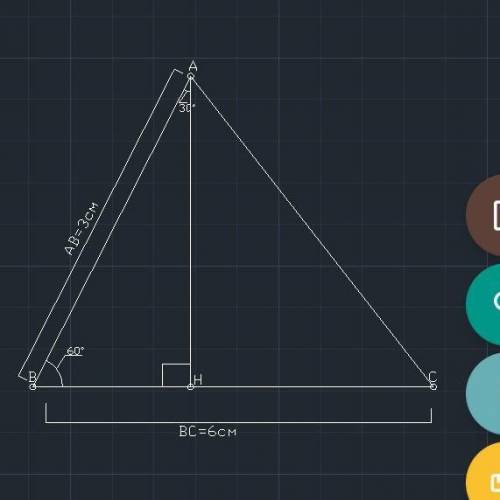
рисунок ниже
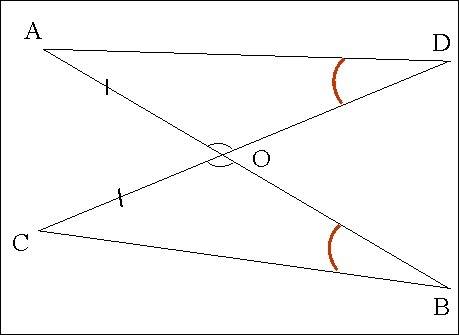
Дано: АВ и CD - прямые
О - точка пересенения
AB = CD
AO = CO
Доказать: а) Δ BOC= Δ DOA
б) ∠ ABC = ∠ADC
Доказательство:
а).
1) AB = CD - по условию
AO = CO - по условию
От равных отрезков отнимем равные отрезки, получим отрезки, равные между собой.
AB-AO = CD-CO
OB = OD
2).
Получаем, равенство треугольников Δ BOC= Δ DOA по двум сторонам и углу между ними.
AO = CO - по условию
OB = OD - доказано в первом действии
<AOD = <COB - как вертикальные
∆BOC= ∆ DOA - равенство треугольников доказано.
б) Из равенства ∆BOC= ∆ DOA
следует равенство соответственных углов, т.е.
< ОBC=<ADО;
< DAО=<ОCВ;
Из равенства углов < ОBC=<ADО;
следует равенство соответственных углов, т.е.
< ABC=<ADC - что и требовалось доказать.