Высота равнобедренной трапеции равна h, а угол между диагоналями,
противолежащий боковой стороне, равен α. Найти площадь трапеции
Диагонали равнобокой трапеции равны, углы, образуемые при основаниях диагоналями, также равны.
Угол α - внешний угол угла АОD треугольника АОD.
Так как внешний угол равен сумме внутренних не смежных с ним углов,
то углы при основании AD равнобедренного треугольника АОD равны половине угла α каждый.
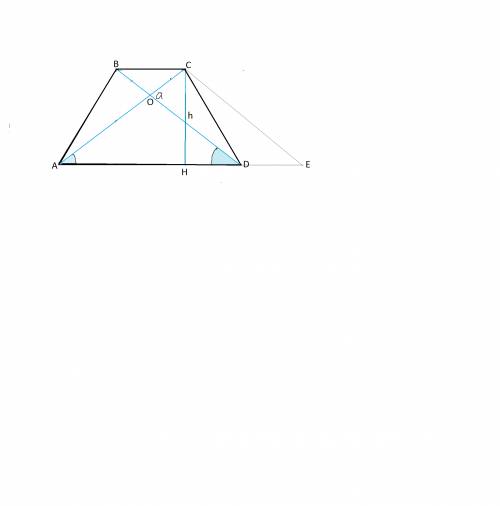
Из вершины С трапеции проведем параллельно BD прямую СЕ до пересечения с продолжением АD.
Четырехугольник ВСED- параллелограмм, DЕ=ВС, и
АЕ равна AD+ВС, то есть сумме оснований трапеции.
Треугольник АСЕ - равнобедренный, т.к. диагонали равнобокой трапеции равны и АС=СЕ, а высота СН в нем - медиана. АЕ=2 АН
АН=СН:tg(α:2)=h:tg(α:2)
Площадь трапеции равна произведению высоты на полусумму оснований.
Полусумма оснований трапеции = АН.
Площадь треугольника АСЕ равна площади трапеции, так как АЕ= сумме ее оснований.
S трапеции равна СН·АН= h·h:tg(а:2) =h²:tg(а:2)
1 угол А-х, В-4х, С 4х-90
х+4х+4х-90=180
9х=270
х=30 В=120 С=30 и стороны равны так как лежат напротив равных углов
2. С
В А Д
угол САВ=180-угол САД (120)=60
угол ВСА=90-60=30град сторона АВ лежит напротив угла 30 град и равна половине гипотенузы АС=2*5=10
3. получаешь равные прямоугольные треугольники: гипотенцузы равны половине основания тр-ка и прилежащие к ней острые углы равны. Один угол угол при основании равнобедренного тр-ка, а втор0й 90-угол1
ΔАВD. Катет, который лежит против угла 30°, равен половине гипотенузы.
ВD равен половине АВ. Значит ВD=АВ/2=6/2=3.
Определим площадь ΔАВС по формуле
S= 0,5·ВD·АС=0,5·3·8=12 см².
ответ: 12 см²