Объяснение:
№1Пусть дан ΔABC, тогда
AB, АС - боковые стороны треугольника
BC - основание треугольника
AB=AC - треугольник равнобедренный
Пусть х будет основание треугольника.
Тогда х+30 будет боковая сторона треугольника.
Периметр равен 150 см.
Составим и решим уравнение (найдём основание треугольника):
х+х+30+х+30=150
3х+60=150
3х=150-60
3х=90
х=90/3
х=30 см.
Боковая сторона треугольника будет равна х+30=30+30=60 см.
ответ: AB=AC=60 cм, ВС= 30 см.
№2Пусть дан ΔABC, тогда
AB, АС - боковые стороны треугольника
BC - основание треугольника
AB=AC - треугольник равнобедренный
Пусть х будет основание треугольника.
Тогда 3х будет боковая сторона треугольника.
Периметр равен 49 см.
Составим и решим уравнение (найдём основание треугольника):
х+3х+3х=49
7х=49
х=49/7
х=7 см.
Боковая сторона треугольника будет равна 3х=7*3=21 см.
ответ: AB=AC=21 cм, ВС=7 см.
0,5 см
Объяснение:
Заметим, что по рисунку 2 клетки= 1 см. Но решать удобнее в клетках, а окончательный ответ перевести в сантиметры.
Так как треугольник прямоугольный и катеты у него равны 3 и 4 клеткам, то гипотенуза равна 5 клеткам (Это так называемый египетский треугольник).
Площадь данного треугольника равна половине произведения катетов, так как треугольник прямоугольный.
S=3*4:2=6 квадратных клеток.
Полупериметр этого треугольника равен: p=(3+4+5):2=12:2=6 клеток.
По формуле радиуса вписанной окружности
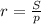 .
.
Подставим известные значения
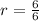 ,
,
r=1 клетка.
То есть r=1:2 см или r=0,5 см.
Два треугольника могут отличаться друг от друга по длине сторон, по градусной мере углов, но их расположение на плоскости не влияет на равенство или неравенство треугольника.