Из точки к плоскости проведены две наклонные одна из которых на 6 см длиннее другой.проекции наклонных равны 17 и 7 см. найдите наклонные

👇

Увидеть ответ

Ответ:

masha1248

21.12.2022

AB - расстояние от точки А до плоскости.

BC=7; DB=17; AC - меньший отрезок; AD - больший отрезок.

Пример AB за X.

AC за Y, тогда AD - y+6

По теореме Пифагора:

AB^2+CB^2=AC^2

AB^2+DB^2=AD^2

Т.е получится:

X^2+49=Y^2

X^2+289=Y^2+12Y+36

Вычтем из нижнего верхнее:

X^2+289-X^2-49=Y^2+12Y+36-Y^2

240=36+12Y

204=12Y

Y=17

За Y мы приняли меньший отрезок, тогда больший будет 17+6=23

Из точки к плоскости проведены две наклонные одна из которых на 6 см длиннее другой.проекции наклонн

4,7(83 оценок)

Открыть все ответы

Ответ:

leomessi1321

21.12.2022

Что такое рельеф. Поверхность земной коры неровная. На одних ее участках возвышаются горы или располагаются равнины, на других — глубокие впадины океанов. Именно благодаря таким неровностям на Земле существует суша и жизнь на ней. Если бы поверхность планеты была плоской, она оказалась бы покрытой океаном глубиной 2450 м!

Все неровности поверхности суши и дна морей и океанов называются рельефом.

Формы рельефа. Любая неровность поверхности Земли представляет собой форму рельефа, которая имеет высоту, площадь и очертания. Выпуклые формы рельефа — это горы, возвышенности, холмы на суше и дне океанов, вогнутые — котловины морей и озер, овраги, балки.

Крупнейшие формы рельефа — это материки и впадины океанов, их существование связано со строением земной коры. К крупнейшим формам относятся также горы и равнины. Крупные формы — это хребты и впадины в горах, низменности и возвышенности на равнинах. Средние и мелкие формы представлены оврагами, холмами, кочками, буграми и другими неровностями.

Рельеф поверхности Земли очень сложен, поскольку более мелкие формы накладываются в разных сочетаниях на более крупные. Именно так возникает своеобразный и неповторимый облик поверхности каждого уголка нашей планеты.

Причины разнообразия рельефа. Рельеф очень разнообразен, потому что на поверхность Земли одновременно воздействуют внутренние (глубинные) и внешние силы. Источник энергии внутренних сил — тепло, образующееся в недрах планеты, а внешних — солнечная энергия.

Внутренние силы опускают и поднимают, растягивают и сжимают поверхность, сминают в складки горные породы. Благодаря этим силам возникают крупнейшие и многие крупные формы рельефа. Среди внутренних сил Земли наибольшую роль играют медленные движения земной коры, землетрясения и вулканизм. Внешними силами — водой, ветром, ледниками, человеком — создаются средние и мелкие неровности рельефа. Все формы — и крупные, и мелкие — с течением времени меняют свои очертания. Поэтому любая физическая карта — лишь моментальный снимок вечно меняющегося рельефа.

Рельеф играет огромную роль в формировании природы различных районов Земли. Он влияет на температуру, количество влаги, растительность и животный мир. Воздействует он и на жизнь человека. Люди селятся в основном на равнинах, потому что на них проще вести хозяйство.

Объяснение:

4,7(85 оценок)

Ответ:

natashasheh

21.12.2022

Так как AK - биссектриса, то:
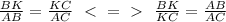
$\frac{BK}{AB}= \frac{KC}{AC} \ \ \textless \ =\ \textgreater \ \ \frac{BK}{KC}= \frac{AB}{AC}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
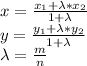
$x= \frac{x_1+\lambda*x_2}{1+\lambda} \\y= \frac{y_1+\lambda*y_2}{1+\lambda} \\\lambda= \frac{m}{n}$
ищем длины AB и AC:
используем формулу:
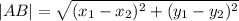
$|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
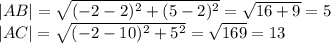
$|AB|=\sqrt{(-2-2)^2+(5-2)^2}=\sqrt{16+9}=5 \\|AC|=\sqrt{(-2-10)^2+5^2}=\sqrt{169}=13$
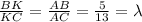
$\frac{BK}{KC}= \frac{AB}{AC}= \frac{5}{13} =\lambda$
находим координаты точки K:
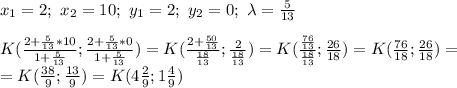
$x_1=2;\ x_2=10;\ y_1=2;\ y_2=0;\ \lambda=\frac{5}{13} \\ \\K( \frac{2+ \frac{5}{13}*10 }{1+\frac{5}{13}} ;\frac{2+ \frac{5}{13}*0 }{1+\frac{5}{13}})=K( \frac{2+ \frac{50}{13} }{ \frac{18}{13}}; \frac{2}{ \frac{18}{13} })=K( \frac{ \frac{76}{13} }{ \frac{18}{13}}; \frac{26}{18} )=K( \frac{76}{18}; \frac{26}{18}) = \\=K( \frac{38}{9}; \frac{13}{9})=K(4 \frac{2}{9};1 \frac{4}{9} )$
теперь определим вид треугольника для этого используем теорему косинусов:
для начала найдем длину BC:
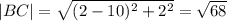
$|BC|=\sqrt{(2-10)^2+2^2}=\sqrt{68}$
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для AC и косинуса угла B
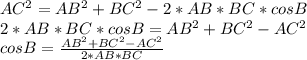
$AC^2=AB^2+BC^2-2*AB*BC*cosB \\2*AB*BC*cosB=AB^2+BC^2-AC^2 \\cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}$
подставим значения:
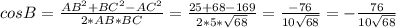
$cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}= \frac{25+68-169}{2*5*\sqrt{68}}= \frac{-76}{10\sqrt{68}} =- \frac{76}{10\sqrt{68}}$
cosB<0 поэтому угол тупой и треугольник тупоугольный
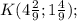ответ: $K(4 \frac{2}{9};1 \frac{4}{9} );\$ треугольник тупоугольный