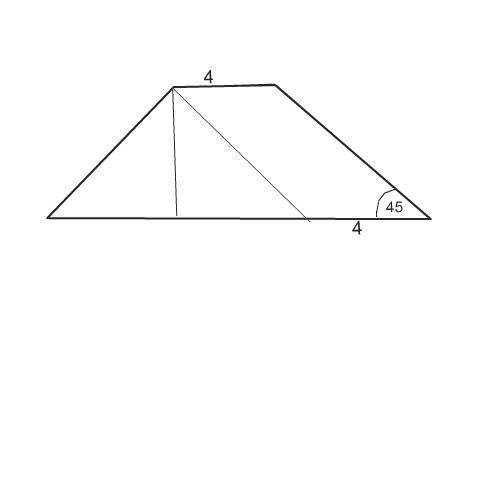
Пусть высота трапеции х
Проведем параллельно боковой стороне прямую. Она отсечет от трапеции прямоугольный равнобедренный треугольник с углами при основании 45 градусов, половина основания которого равна высоте и меньшему основанию.
Тогда большее основание 2х+4
Полусумма оснований
(2х+4+4):2=(2х+8):2=х+4
Площадь трапеции
х(х+4)=117
х²+4х-117=0 Решим это уравнение:
D = b² - 4ac = 484
√D = 22
х1=9
х2= -13 (не подходит)
Боковую сторону по свойству диагонали квадрата и гипотенузы равнобедренного прямоугольного треугольника найдем по формуле
а√2
Она равна 9√2 см
Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам. Поэтому диагонали разбиваеют ромб на 4 равных прямоугольных треугольника. R впис-ой окружности равен высоте, опущенной из вершины прямого угла умноженной на гипотенузу.
Используя т-му Пифагора найдём сторону (все стороны в ромбе равны)
Сторона в квадрате = 15*15+20*20 = 400 + 225 = 625
Каждая сторона ромба = корень из 625 = 25
Проведём из центра (точки О) прямую линию ОМ на сторону ромба, к примеру на АВ ( прямая должна доходить до середины стороны АВ ). Это прямая будет являться радиусом окружности!
Треугольники АВО и АМО подобны
Если треугольники подобны, то : ОМ/ВО = ОА/АВ ОМ = АО*ОВ/АВ = 20*15/25 = 12 см
ответ 12 см
Площадь ромба равна сторона*высота, т. е.
S=a*h, h - это радиус цилиндра
a=S/h
Площадь вращения 2*Pi*h*a=2*Pi*S=1884 дм^2