По заданным величинам находим углы треугольника.
C = arc sin(20/25) = arc sin(4/5) = 53,1301 градуса .
B = arc cos (7/25) = 73,7398 градуса.
Угол А = 180 - В - С = 53,1301 градуса .
Значит, треугольник - равнобедренный: АВ = ВС = 25.
Тогда АС = 2√(25² - 20²) = 2√(625 - 400) = 30.
Находим ДН из условия подобия треугольников НДС и АВД и равенства взаимно перпендикулярных углов НСД и АВД.
ДН/ДС - АД/ВД. Здесь точка Н - точка пересечения высот.
ДН = 15*15/20 = 11,25.
Используя формулу деления высот точкой их пересечения
ВН/НД = cos B/(cos A*cosC), находим отрезки.
Отрезки на сторонах. отсекаемые высотами
АС₂ = 18 С₂B = 7 AB = 25 25
BA₂ = 7 A₂C = 18 BC = 25 25
АB₂ = #ДЕЛ/0! B₂C = #ДЕЛ/0! AC = #ДЕЛ/0! 30
Точка В2 это точка Д, она делит АС пополам,АД = 30/2 = 15.
Далее удобнее решать в прямоугольной системе координат,
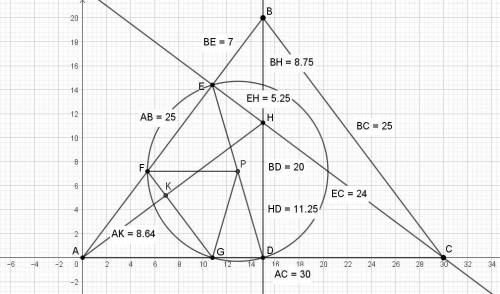
Пусть А(0; 0), В(15; 20), С(30; 0).
Находим координаты точки Е из подобия АЕ к АВ = 18/25.
х(В) = 15*(18/25) = 54/5 = 10,8.
у(В) = 20*(18/25) = 72/5 = 14,4. Точка E(10,8; 14,4), точка Д(15; 0).
Находим координаты центра Р окружности на ДЕ.
Р = (10,8+15)/2; (14,4+0)/2) = (12,9; 7,2).
Радиус окружности равен РЕ = √(15-12,9)² + (0-7,2)²) = 7,5.
Уравнение окружности (x-12,9)² + (y-7,2)² = 7,5².
Уравнение прямой АВ по угловому коэффициенту: у = (20/15)х или у = (4/3)х.
Находим координаты точки F как точки пересечения АВ с окружностью, решая систему:
{ у = (4/3)х.
{ (x-12,9)² + (y-7,2)² = 7,5². После подстановки у= (4/3)х во второе уравнение находим х = 27/5 = 5,4, а у = 36/5 = 7,2.
Второй корень повторяет координаты точки Е(10,8; 14,4).
Координаты точки G находим аналогично, толь как точку пересечения с осью Ох в виде уравнения у = 0.
G(10.8; 0). Второй корень повторяет координаты точки D(15; 0).
Уравнение прямой АН: у = (11,25/15)х.
Уравнение GF. Вектор GF = (5,4; -7,2).
Уравнение GF:( (x - 10,8)/5,4) = y/(-7,2).
Координаты точки К находим как точку пересечения прямых АН и GF, решая систему:
{ у = (11,25/15)х.
{ ( (x - 10,8)/5,4) = y/(-7,2).
Решение даёт значение х(К) = 6,912, у(К) = 5,184.
Длина АК = √(6,912² + 5,184²) = 8,64.
ответ: АК = 8,64.
Площадь S1 боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на её боковое ребро. Плоскость перпендикулярного сечения пересекает боковые грани по их высотам. Поэтому периметр перпендикулярного сечения равен сумме этих высот, т. е. 3*2=6.
Значит, S1 = 3al = 18
ПустьS -- площадь основания призмы. Площадь ортогональной проекции основания призмы на плоскость, перпендикулярную боковым рёбрам, равна площади перпендикулярного сечения, делённой на косинус угла между плоскостями основания и перпендикулярного сечения. Этот угол равен углу между боковым ребром и высотой призмы, т. е. 60∘.
Поэтому
S2= 2√3Следовательно, площадь полной поверхности призмы равна
Решение на фото//////