Два треугольника равны по третьему признаку равенства треугольников, если ...
Выберите один из 3 вариантов ответа:
1) две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника ;
2) сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника ;
3) три стороны одного треугольника соответственно равны трём сторонам другого треугольника.
ответ: 3).Задание №2.Дано:ΔABD и ΔCBD;
AB = BC;
AD = DC.
Доказать:ΔABD = ΔCBD
Доказательство:1. AB = BC (по условию) |
2. AD = DC (по условию |⇒ ΔABD = ΔCBD (по третьему признаку).
3. BD - общая сторона |
Что и требовалось доказать!
ответ: 2).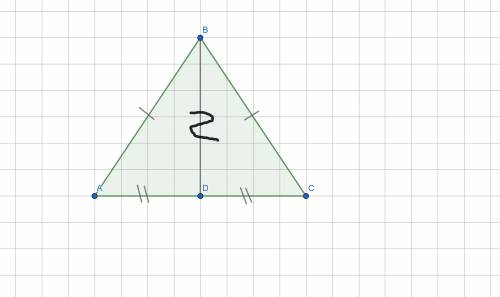
S = ab.
Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью S.
Докажем, что S = ab.
Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке 1.
Так как площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна (a + b)2.
С другой стороны, этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (так как, по свойству площадей, равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. Так как четырехугольник составлен из нескольких четырехугольников, то, по свойству площадей, его площадь равна сумме площадей этих четырехугольников:
(a + b)2 = S + S + a2 + b2, или a2 + 2ab + b2 = 2S + a2 + b2.
Отсуда получаем: S = ab, что и требовалось доказать.