В треугольнике АВС (АВ=ВС) проведем высоту АН к стороне ВС. Высота тупоугольного треугольника, проведенная из вершины острого угла, лежит вне треугольника.
В равнобедренном ∆ АВС ∠ВСА=∠САВ= 30°,⇒ ∠В=180°-2•30°=120° В Δ АВН угол АВН смежный углу АВС равен 180°-120°=60°. Угол ВАН=180°- 90°-60°=30°.
Примем АВ=ВС равными а. Тогда ВН=а•sin30°=a/2, AH=a•sin60°=a√3/2.
Биссектриса АЕ делит угол ВАС на два по 30°:2=15°. Тогда в прямоугольном треугольнике НАЕ ∠НАЕ=<НАВ+ <ВАЕ=30°+15°=45°. Сумма острых углов прямоугольного треугольника 90°, поэтому ∠НЕА=45°⇒ ∆ АНЕ - прямоугольный равнобедренный (по свойству), и ЕН=АН=a√3/2
НЕ=ВЕ+ВН=(8+а/2 )
Из равенства АН=ЕН следует a√3/2=8+а/2, откуда получим а-8=8√3, ⇒ а=8(√3+1) см
Площадь равнобедренного треугольника равна половине произведения равных сторон на синус угла между ними.
S(ABC)=0,5•a²•sin120°. S(ABC)=0,5•[8(√3+1)]²•√3/2=32√3( 2+√3) см²

Определение 1. Двугранным углом называется фигура, образованная двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу – прямую а. Величина двугранного угла равна его линейному углу.
Определение 2. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Расстояние от точки до прямой и от точки до плоскости равно длине проведенного между ними перпендикуляра.
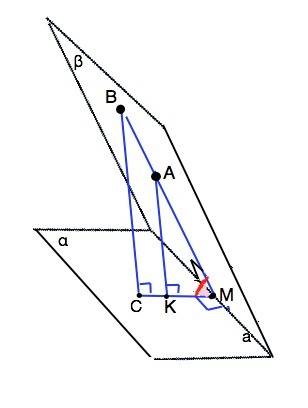
Обозначим грани угла α и β, ребро - а Пусть точки А и В лежат в плоскости грани β. Длина перпендикуляра ВМ=6√2, перпендикуляра AM=4√2.
Опустим из т.А и т.В перпендикуляры ВС и АК на грань α. ВМ - наклонная, СМ - ее проекция на плоскости грани α. По т. о 3-х перпендикулярах СМ⊥ребру а. ⇒ Угол ВАС - искомый.
В треугольнике ВМС отрезки АК||ВС, ⇒ острые углы прямоугольных ∆ ВСМ и АМК равны, эти треугольники подобны.
По условию ВС+АК=10 см Примем длину АК=х см. Тогда ВС=10-х см. Из подобия следует отношение х:(10-х)=4√2:6√2, ⇒ х•6√2=(10-x)•4√2. Откуда получим 5х=20 см, х=4 см. Из прямоугольного треугольника АКМ sinAMK=АК:АМ=4:4√2=1/√2, что равно √2/2, – синусу 45°. Величина данного двугранного угла 45°.