Отрезки МК и NP параллельны соседним сторонам прямоугольника, => соответственно равны им, пересекаются под прямым углом и делят АВСD на 4 прямоугольника, (неважно, равной или разной площади). Обозначим точку пересечения МК и NP буквой О.
а)
Стороны четырехугольника МNKP являются диагоналями получившихся прямоугольников и делят каждый из них пополам (свойство). Поэтому площадь MNKP равна сумме площадей этих половин, т.е. равна половине площади ABCD.
б)
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Так как S(ABCD)=AB•CD, МК=АD и NP=AB, а sin90°=1, то S(MNKP)=MK•NP•sin90°=0,5•S(ABCD).
в)
S(MNKP)=S∆MNP+S∆NKP=0.5•MO•NP+0.5•KO•NP=0,5•NP•(MO+OK) => S(MNKP)=0,5•NP•MK =>
S(MNKP) =0,5•S(ABCD), т.к. NP=AB и МК=АD
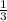BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=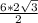
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V=9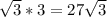
Угол А = 30°
Против угла в 30° лежит катет равный половине гипотенузы.
BH = BA/2 = 16/2 = 8 (см)
Площадь трапеции:
S = ((BC+AD)/2) * BH = 160 (см²)
ответ: 160 см².
[В чёрном прямоугольнике формула нахождения площади трапеции: полусумма оснований умноженная на высоту]