1) данные треугольники подобны, т.к углы ВАС и В1А1С1 равны, а стороны АВ и АС первого треугольника пропорциональны сторонам А1В1 и А1С1 соответственно АВ/А1В1=АС/А1С1=2/3. (по 2 признаку подобия)
Тогда угол С1= углу С= 71°. ВС/В1С1=2/3. В1с1=ВС×3/2=10×3/2=15.
2)треугольники подобны по 3 признаку подобия: АВ:А1В1=АС:А1С1=ВС:В1С1=2/1 (т.к. 10а/5а=2, 14в/7в=2 и 12с/6с=2)
Угол С=180°-угол А-угол В. Угол В= углу В1=40°. Угол С=180-80-40=60°. Угол С1=углу С=40°.
(Соответсвенные углы подобных треугольников равны)
3) треугольники ABC и MBN подобны по 1 признаку угол В общий, угол ВМN= BAC- соответственные (это если АС и NM параллельны по условию мало данных) тогда BM:AB=BN:BC=MN:AC. Возьмем ВМ за х. Тогда АВ - х+3. ВС=8+4=12. BM:AB=MN:AC. x:(x+3):10:15. x:(x+3)=2/3. 2×(x+3)=3x. 2x+6=3x. -x=-6, x=6.
BM=6
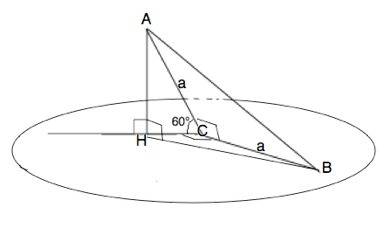
Через катет прямоугольного равнобедренного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 60°. Найдите углы, которые образуют 2 другие стороны треугольника с этой плоскостью.
Обозначим треугольник АВС. АС=ВС, угол С=90°
Проведенная плоскость и плоскость треугольника образуют двугранный угол, линейным углом которого являются два перпендикуляра к его ребру в точке С.
Угол АСВ - прямой, ⇒АС- перпендикуляр в плоскости треугольника к линии пересечения плоскостей, НС - перпендикуляр, проведенный в проведенной плоскости к той же линии.
Угол АСН =60°
АН - перпендикуляр к плоскости, НВ - проекция гипотенузы АВ на плоскость.
Угол АВН - искомый.
В равнобедренном прямоугольном треугольнике острые углы равны 45°.
Примем катеты ∆ АВС равными а. Тогда гипотенуза
АВ=а:sin 45°=a√2
АН=а•sin60°=a√3/2
sinАВН=АН:АВ=a√3/2):a√2=0,61237
Это синус угла ≈37,76°
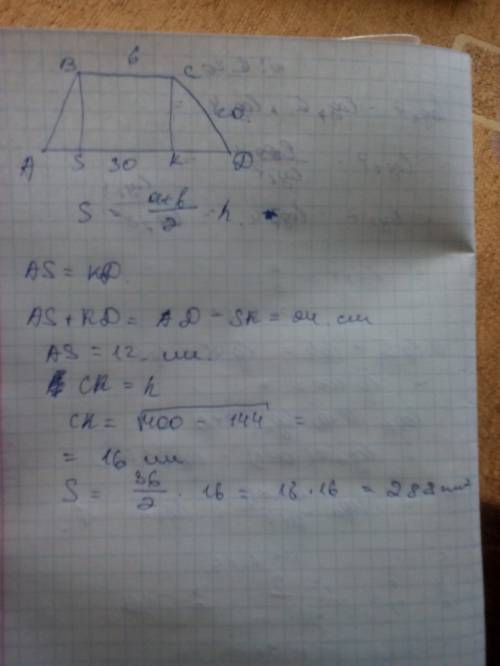
По теореме Пифагора, высота равна:
√(20²-12²)=√256=16
S=(30+6)/2*16=18*16=288
ответ:288 см²