1872шт.
Объяснение:
Для того чтобы узнать количество дощечек необходимо площадь пола поделить на площадь дощечки (обязательно чтобы площади были одинаковой ед. изменения, если пол в метрах, то и дощечки должны быть в метрах.)
Находим площадь пола (площадь прямоугольника равна произведению длины на ширину)
Sп.=11,7*4,8=56,16 м² площадь пола.
Переводим ед. измерения в одинаковую величину.
1м=100см.
30см=30/100=0,3 м
10см=10/100=0,1м .
Находим площадь дощечки.
Sд.=0,3*0,1=0,03 м² площадь дощечки.
Количество дощечек равно Sп/Sд.
56,16:0,03=1872 шт.
ответ 1872шт.
Обозначение:
Sп.- площадь пола
Sд.- площадь дощечки.
Иногда в таких задачах получается не целое число, тогда округлить нужно всегда в большую сторону. Например у вас получилось 1872,3, округлить в большую сторону 1873.
Будем считать, что задание дано так:
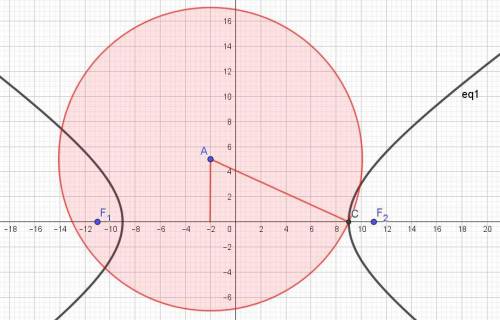
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
∠ABD = ∠B - ∠CBD = 120° - 90° = 30°. Тогда AD = 1/2AB => AB = 2AD = 24 см.
По теореме Пифагора:
BD = √AB² - AD² = √24² - 12² = √576 - 144 = √432 = 12√3 см.
OC = OA, BO = OD, т.к. диагонали точкой пересечения делятся пополам. BO = 6√3 см.
AD = BC = 12 см, т.к. противоположные стороныр параллелограмма равны.
По теореме Пифагора:
CO = √CB² + BO² = √144 + 108 = √252 = 6√7 см.
CA = 2CO = 12√7 см.
SCOD = 1/2CB•OD = 1/2•12см•6√3см = 36√2 см².
Оьвет: 12√3 см, 12√7 см, 36√3 см².