
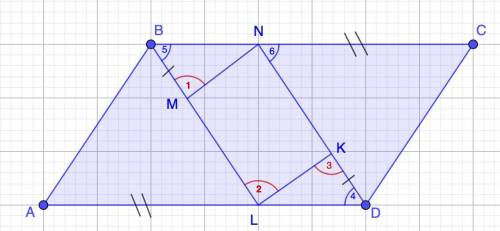
Объяснение:
Дано: MNKL - параллелограмм.
AL=NC; BM=KD.
Доказать: ABCD - параллелограмм.
Доказательство:
MNKL - параллелограмм. ⇒ MN║KL и ML║NK.
1) Рассмотрим ΔMBN и ΔLKD.
KD=MB (по условию)
MN=LK (свойство параллелограмма)
∠1=∠2 (соответственные при NM║LK и секущей BL.
∠3=∠2 (накрест лежащие при LB║ND и секущей LK.
⇒∠1=∠3.
ΔMBN и ΔLKD (по двум сторонам и углу между ними, 1 признак)
⇒ LD=BN; ∠5=∠4 (как соответственные элементы)
2) AD=AL+LD
BC=BN+NC
⇒AD=BC
3) ∠5=∠4 (п.1)
∠5=∠6 (соответственные при BL║DN и секущей ВС)
⇒∠4=∠6 - накрест лежащие при ВС и AD и секущей ND;
⇒ ВС ║ AD.
4) AD=BC (п.2)
ВС ║ AD (п.3)
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.
⇒ABCD - параллелограмм
Боковая поверхность - 3 трапеции, средняя линяя у каждой из трех - 4;
2 из них - с высотой 1;
грань, "противоположная" ребру длинны 1, - это равнобедренная трапеция, её высоту и надо вычислить, чтобы получить ответ.
проводим "вертикальную" плоскость через ребро 1, делящую основания "пополам" (то есть эта плоскость проходит через высоты оснований пирамиды, выходящие из вершин ребра 1).
сечение пирамиды, которое получится - это трапеция с боковой стороной 1, перпендикулярной основаниям, и основаниями 3*sqrt(3)/2 и 5*sqrt(3)/2. четвертая сторона легко вычисляется, и равна 2. Это и есть высота наклонной грани трапеции (поскольку сечение перпендикулярно основаниям пирамиды);
ответ S = 4*1+4*1+4*2 = 16