Четырёхугольник abcd со сторонами ab = 5 и cd = 17 вписан в окружность. диагонали ac и bd пересекаются в точке k, причём найдите радиус окружности, описанной около этого четырёхугольника.

👇

Увидеть ответ

Открыть все ответы

Ответ:

katya8631

09.07.2020

A1.

Sшестиугольника =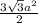 $\frac{3\sqrt{3} a^2}{2}$

ответ: 4

A2.

Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:

$S = 4 (\frac{R * R}{2} )$ = 2 R^2

ответ: 1

A3.

Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):

$R = \frac{a\sqrt{3} }{2}$

$a = \frac{2R}{\sqrt{3}}$

Площадь одного треугольника будет равна:

$S = \frac{a^2\sqrt{3} }{4}$ $= \frac{4R^2\sqrt{3} }{3*4} = \frac{R^2\sqrt{3}}{3 }$

Площадь шестиугольника:

$S_w = \frac{6R^2\sqrt{3} }{3} = 2R^2\sqrt{3}$

ответ: 2

B1.

Пусть вписанный треугольник - ΔABC, сторона = ; описанный - ΔA₁B₁C₁, сторона - a_1

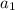
Для ΔA₁B₁C₁ радиус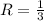 $R = \frac{1}{3}$ высоты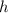

$h^2 = a^2 - (\frac{1}{2} a)^2 = a^2 - \frac{1}{4} a^2 = \frac{3a^2}{4} \\h = \frac{a\sqrt{3} }{2}$

$R = \frac{a\sqrt{3} }{2} * \frac{1}{3} = \frac{a\sqrt{3} }{6}$ ⇒

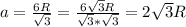
⇒ $a = \frac{6R}{\sqrt{3} } = \frac{6\sqrt{3}R}{\sqrt{3}*\sqrt{3}} = 2\sqrt{3}R$

$P = 3a; P_{A_1B_1C_1} = 3 * 2\sqrt{3} R = 6\sqrt{3} R$

$S = \frac{1}{2} a*h; S_{A_1B_1C_1} = \frac{1}{2} * 2\sqrt{3} R * \frac{2\sqrt{3} R * \sqrt{3} }{2} = \frac{4*3*\sqrt{3} R^2}{4} = 3\sqrt{3} R^2}$

Для ΔABC радиус R =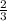 $\frac{2}{3}$ высоты :

$R = \frac{a\sqrt{3} }{2} * \frac{2}{3} = \frac{a\sqrt{3} }{3}$ ⇒

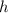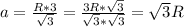
⇒ $a = \frac{R * 3}{\sqrt{3} } = \frac{3R * \sqrt{3} }{\sqrt{3} * \sqrt{3} } = \sqrt{3} R$

$P_{ABC} = 3\sqrt{3} R\\S_{ABC} = \frac{1}{2} * \sqrt{3} R * \frac{\sqrt{3}R*\sqrt{3}}{2} = \frac{3R^2 * \sqrt{3}}{4}$

Найдем соотношение периметров и площадей:

$S_{A_1B_1C_1} : S_{ABC} = 3\sqrt{3}R^2 : \frac{3R^2\sqrt{3} }{4} = 4: 1\\P_{A_1B_1C_1} : P_{ABC} = 6\sqrt{3}R : 3\sqrt{3}R = 2 : 1$

4,6(89 оценок)

Ответ:

AmiKot1105

09.07.2020

Если нам известны стороны:
Проведем две медианы к боковым сторонам треугольника.
Так как он равнобедренный, медианы эти равны и отсекают от исходного треугольника два меньших, равных между собой.
Угол при основании неизвестен, поэтому обозначим его α и его косинус - cosα
Выразим медиану одного из образовавшихся треугольников по теореме косинусов.
Чтобы найти косинус угла при основании, применим теорему косинусов к данному в условии задачи треугольнику, стороны которого известны.
Подставив найденное значение cosα в уравнение медианы, найдем ее длину.

Контретное решение зависит от того, какие даны величины в условии задачи.

4,5(26 оценок)

Это интересно:

Кулинария-и-гостеприимство

02.05.2023

Как сварить овощи: простые рецепты и полезные советы...

Питомцы-и-животные

20.02.2021

Как определить пол хомячка...

Стиль-и-уход-за-собой

30.08.2020

Как справиться с месячными...