Question

1! 30 . докажите равенство треугольников по медиане и углам,которые она образует со стороной треугольника, к которой она проведена, и углам, которые она образует со сторонами угла, из вершины которого она проведена.

Answer 1

Рассмотрим ∆BCM и ∆B1C1M1.
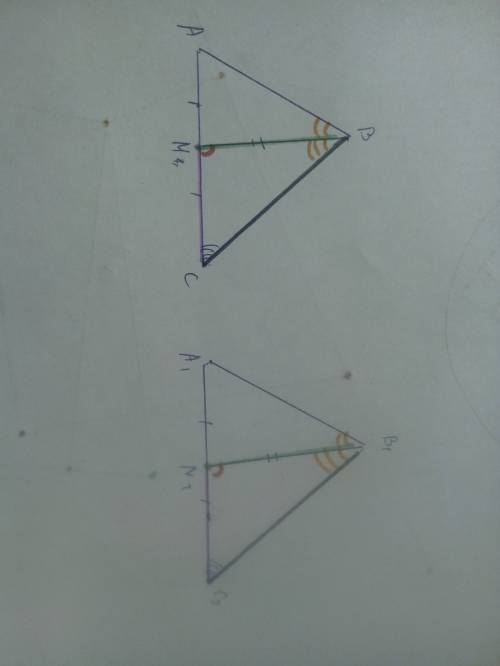
MB = BM1
∠CBM = ∠C1B1M1
∠BMC = ∠B1M1C1 (все эти три равенства по условию даны).
Значит, ∆BCM = ∆B1C1M1 - по II признаку.
Из равенства треугольников следует, что∠С = ∠С1, ВС = В1С1 И MC = M1C1.
Т.к. BM - медиана, то AM = MC.
Т.к. B1M1 - медиана, то A1M1 = M1C1.
MC = M1C1 => AM = MC = A1M1 = M1C1. Тогда AC = 2MC = 2M1C1 = A1C1.
Рассмотрим ∆ABC и ∆A1B1C1.
ВС = В1С1
АС = А1С1
∠С = ∠С1
Значит, ∆ABC = ∆A1B1C1 - по I признаку.

Answer 2

Продлим медианы так, чтобы: BD = DO, B1D1 = D1O1. В ΔADO и ΔDBC: AD = DC (из условия) BD = DO (по построению) ∠ADO = ∠BDC (как вертикальные).
Таким образом, ΔADO = ΔBDC по 1-му признаку равенства треугольников; откуда АО = ВС как лежащие в равных треугольниках против равных углов, ∠AOD = ∠DBC.
Аналогично ΔA1D1O1 = ΔD1B1O1 и А1О1 = В1С1, ∠A1O1D1 = ∠D1В1С1.
Т.к. ВС = В1С1, то АО = А1О1. В ΔАОВ и ΔА1О1В1: АВ = А1В1 (из условия), АО = А1О1 (по построению), ВО = В1О1 (по построению),

Таким образом, ΔАВО = ΔА1В1О1 по 3-му признаку равенства треугольников. Откуда

∠A1B1C1 = ∠A1B1D1 + ∠D1B1C1, т.к. правые части равны, то и левые должны быть равны.
Следовательно ∠АВС = ∠А1В1С1.
В ΔABC и ΔA1В1С1:
∠АВС = ∠А1В1С1, АВ = А1В1, ВС = В1С1 (из условия).
Таким образом, ΔАВС = ΔА1В1С1 по 1-му признаку равенства треугольников, что и требовалось доказать.