етрия. 8 класс. тест 4. вариант 1.
в δ авс ∠асв = 90°. ас и вс — катеты, ав — гипотенуза.
cd — высота треугольника, проведенная к гипотенузе.
ad — проекция катета ас на гипотенузу,
bd — проекция катета вс на гипотенузу.
высота cd делит треугольник авс на два подобных ему (и друг другу) треугольника: δ adc и δ cdb.
из пропорциональности сторон подобных δ adc и δ cdb следует:
ad : cd = cd : bd. отсюда cd2 = ad ∙ bd. говорят: высота прямоугольного треугольника, проведенная к гипотенузе, есть средняя пропорциональная величина между проекциями катетов на гипотенузу.
из подобия δ adc и δ аcb следует:
ad : ac = ac : ab. отсюда ac2 = ab ∙ ad. говорят: каждый катет есть средняя пропорциональная величина между всей гипотенузой и проекцией данного катета на гипотенузу.
аналогично, из подобия δ сdв и δ аcb следует:
bd : bc = bc : ab. отсюда bc2 = ab ∙ bd.
решите :
1. найти высоту прямоугольного треугольника, проведенную к гипотенузе, если она делит гипотенузу на отрезки 25 см и 81 см.
a) 70 см; b) 55 см; c) 65 см; d) 45 см; e) 53 см.
2. высота прямоугольного треугольника, проведенная к гипотенузе, делит гипотенузу на отрезки 9 и 36. определить длину этой высоты.
a) 22,5; b) 19; c) 9; d) 12; e) 18.
4. высота прямоугольного треугольника, проведенная к гипотенузе, равна 22, проекция одного из катетов равна 16. найти проекцию другого катета.
a) 30,25; b) 24,5; c) 18,45; d) 32; e) 32,25.
5. катет прямоугольного треугольника равен 18, а его проекция на гипотенузу 12. найти гипотенузу.
a) 25; b) 24; c) 27; d) 26; e) 21.
6. гипотенуза равна 32. найти катет, проекция которого на гипотенузу равна 2.
a) 8; b) 7; c) 6; d) 5; e) 4.
7. гипотенуза прямоугольного треугольника равна 45. найти катет, проекция которого на гипотенузу равна 9.
8. катет прямоугольного треугольника равен 30. найти расстояние от вершины прямого угла до гипотенузы, если радиус описанной около этого треугольника окружности равен 17.
a) 17; b) 16; c) 15; d) 14; e) 12.
10. гипотенуза прямоугольного треугольника равна 41, а проекция одного из катетов 16. найти длину высоты, проведенной из вершины прямого угла к гипотенузе.
a) 15; b) 18; c) 20; d) 16; e) 12.
a) 80; b) 72; c) 64; d) 81; e) 75.
12. разность проекций катетов на гипотенузу равна 15, а расстояние от вершины прямого угла до гипотенузы равно 4. найти радиус описанной окружности.
a) 7,5; b) 8; c) 6,25; d) 8,5; e) 7.
сверить ответы!
последние тесты 6.3.06. умножение отрицательных чисел. примеры с десятичными дробями.6.3.04. сложение чисел с разными знаками. примеры с обыкновенными дробями.6.3.03. сложение чисел с разными знаками. примеры с десятичными дробями.6.3.02. сложение отрицательных чисел. примеры с обыкновенными дробями.6.3.01. сложение отрицательных чисел. примеры с десятичными дробями.архивы выберите месяц октябрь 2016 сентябрь 2016 апрель 2016 январь 2016 ноябрь 2015 октябрь 2015 март 2015 февраль 2015 декабрь 2014 октябрь 2014 сентябрь 2014 август 2014 июнь 2014 май 2014 апрель 2014 март 2014 февраль 2014 январь 2014 декабрь 2013 ноябрь 2013 октябрь 2013 сентябрь 2013 май 2013 апрель 2013 март 2013 февраль 2013 в видео.мой электронный адрес: [email protected] андрющенко татьяна яковлевнарубрики -10 (6)-11 (4)-7 (14)-8 (8)-9 (8)-10 (1)-11 (1)-7 (3)-8 (4)-9 (2)ент-2013 (20)ент-2014 (25)-5 (3)-6 (9)новости (13)огэ (6)
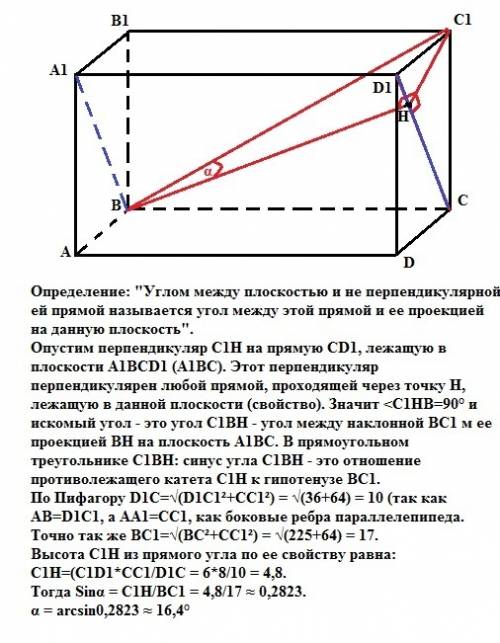
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
с самой южной так же- это южный полюс- 90 градусов южной широты, долгота не определена